GWDR 模型即“地理加权密度回归模型”,其原理是对每个坐标维度分别进行加权,使用总权重进行加权回归。 本文主要介绍函数 gwdr() 的用法。
基本用法
我们以示例数据 LondonHP 为例,展示函数 gwdr() 的用法。 假设我们以 PURCHASE 为因变量,FLOORSZ, PROF 和 UNEMPLOY 为自变量,可以使用下面的方式构建 GWDR 模型。
data(LondonHP)
m1 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP
)
m1
Geographically Weighted Density Regression Model
================================================
Formula: PURCHASE ~ FLOORSZ + UNEMPLOY + PROF
Data: LondonHP
Dimension-specified Weighting Configuration
-------------------------------------------
bw unit kernel
X 0.618 % gaussian
Y 0.618 % gaussian
Summary of Coefficient Estimates
--------------------------------
Coefficient Min. 1st Qu. Median 3rd Qu. Max.
Intercept -193327.404 -175567.666 -168977.411 -162922.380 -140786.788
FLOORSZ 1305.212 1393.038 1467.604 1576.467 1696.385
UNEMPLOY 523550.252 580577.144 642590.758 718386.733 824739.610
PROF 330854.107 351258.803 368915.791 388013.724 413800.564
Diagnostic Information
----------------------
RSS: 494470388228
ENP: 10.34202
EDF: 305.658
R2: 0.7238836
R2adj: 0.7145105
AIC: 7594.609
AICc: 7604.972
这里展示的是在不进一步设置变量的情况下调用函数,函数默认以如下配置设置算法
- 每个维度的带宽大小为 61.8% 样本数
- 每个维度都采用可变带宽
- 每个维度都采用高斯核函数
- 不优选带宽
大多数情况下,这样设置可以保证算法能够运行。如需进一步定制参数,请参考加权配置
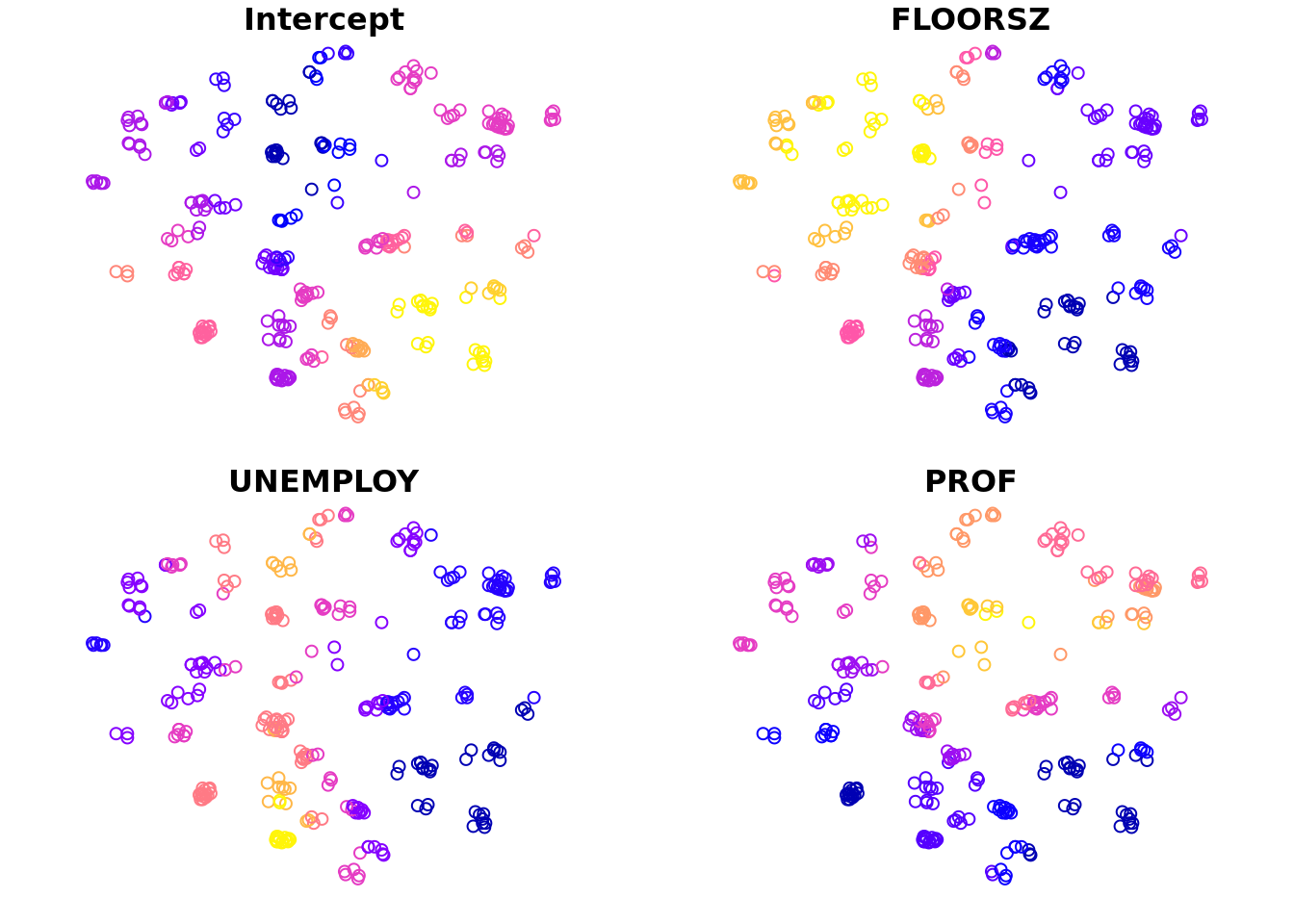
该函数返回一个 gwdrm 的对象,通过控制台输出信息,我们可以得到 调用的表达式、数据、带宽、核函数、系数估计值的统计、诊断信息。 同样,也支持使用 coef() fitted() residuals() 等函数获取信息。
Intercept FLOORSZ UNEMPLOY PROF
0 -156686.3 1360.666 665222.6 349001.4
1 -156301.6 1358.544 662711.3 348652.4
2 -159630.9 1375.525 687318.5 351295.0
3 -159754.8 1376.436 688396.9 351320.4
4 -157435.6 1362.784 671656.0 349629.5
5 -146554.7 1311.270 601273.5 339194.4
[1] 138878.6 136126.3 121082.4 163737.0 179706.1 160977.9
[1] 18121.366 -22626.252 -39332.379 -13737.003 10293.939 -1027.876
此外,与其他函数类似,gwdrm 对象中提供了一个 $SDF 变量保存了系数估计值等一系列局部结果。
Simple feature collection with 6 features and 6 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 531900 ymin: 159400 xmax: 535700 ymax: 161700
CRS: NA
Intercept FLOORSZ UNEMPLOY PROF yhat residual
0 -156686.3 1360.666 665222.6 349001.4 138878.6 18121.366
1 -156301.6 1358.544 662711.3 348652.4 136126.3 -22626.252
2 -159630.9 1375.525 687318.5 351295.0 121082.4 -39332.379
3 -159754.8 1376.436 688396.9 351320.4 163737.0 -13737.003
4 -157435.6 1362.784 671656.0 349629.5 179706.1 10293.939
5 -146554.7 1311.270 601273.5 339194.4 160977.9 -1027.876
geometry
0 POINT (533200 159400)
1 POINT (533300 159700)
2 POINT (532000 159800)
3 POINT (531900 160100)
4 POINT (532800 160300)
5 POINT (535700 161700)
使用该变量,可以进行专题制图。除此之外,改包还提供了一个 plot() 函数,通过输入 gwdrm 对象,可以快速查看回归系数。
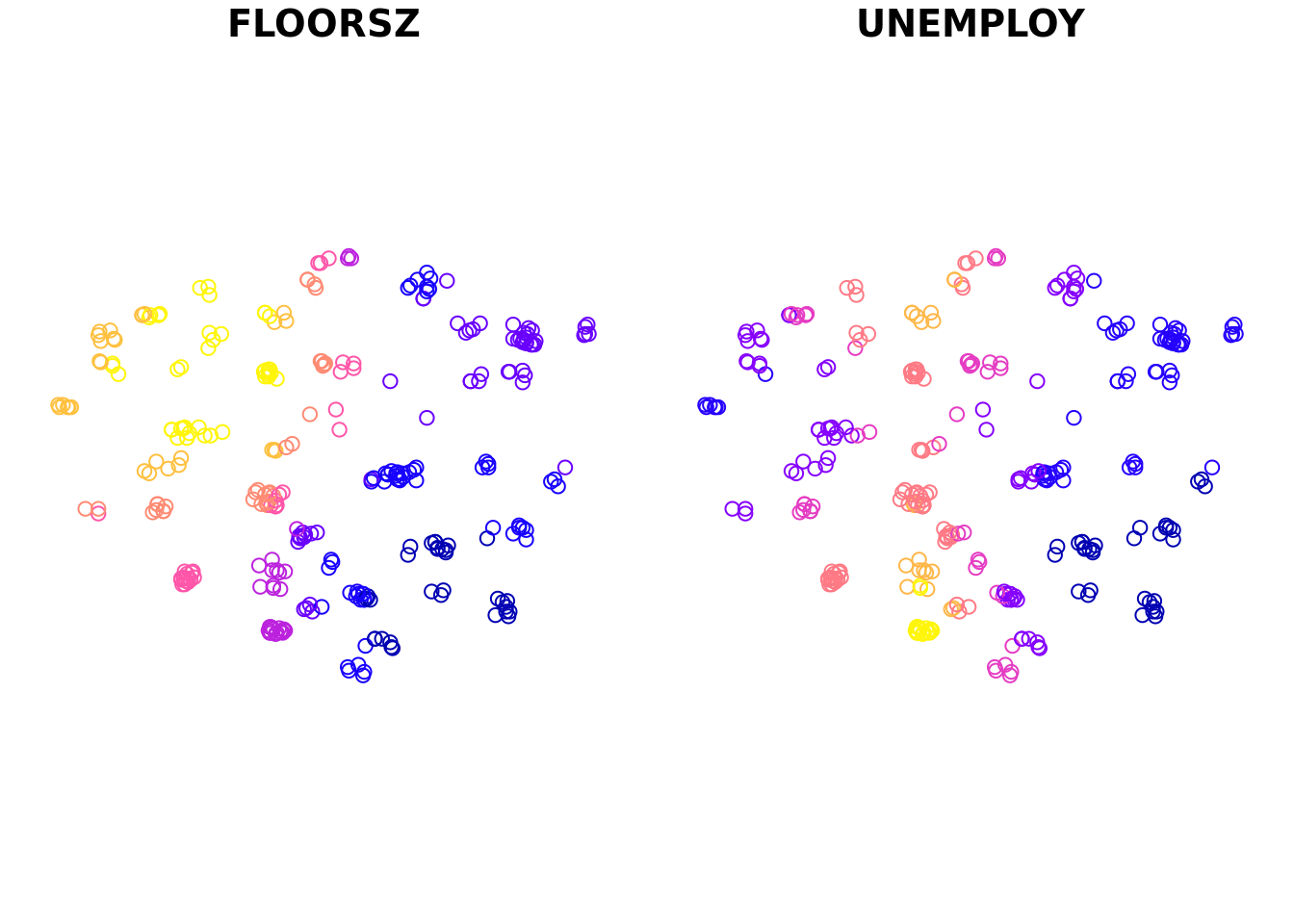
plot(m1, columns = c("FLOORSZ", "UNEMPLOY"))
如果指定了 columns 参数,则仅绘制第二个参数列出的系数,否则绘制所有回归系数。
加权配置
每个维度的加权配置选项
包中定义了一个 GWDRConfig 的 S4 类型,用于提供多尺度加权配置的设置。 该类型的对象包含以下几个成员:
bw |
Numeric |
带宽值。 |
adaptive |
Logical |
是否为可变带宽。 |
kernel |
Character |
核函数名称。 |
使用函数 gwdr_config() 可以直接构造一个对象。
gwdr_config(0.618, TRUE, "bisquare")
An object of class "GWDRConfig"
Slot "bw":
[1] 0.618
Slot "adaptive":
[1] TRUE
Slot "kernel":
[1] "bisquare"
该类型的对象也支持使用 rep() 函数复制,但支持持 times 参数。
rep(gwdr_config(36, TRUE, "bisquare"), 2)
[[1]]
An object of class "GWDRConfig"
Slot "bw":
[1] 36
Slot "adaptive":
[1] TRUE
Slot "kernel":
[1] "bisquare"
[[2]]
An object of class "GWDRConfig"
Slot "bw":
[1] 36
Slot "adaptive":
[1] TRUE
Slot "kernel":
[1] "bisquare"
使用 GWDRConfig 进行参数配置
函数 gwdr() 既可以统一设置加权配置项,也可以分别设置加权配置项。
统一设置
如果要给所有维度统一设置加权配置项,可以传入只包含一个 GWDRConfig 类型对象的列表。 例如,下面的代码将所有维度的带宽大小设置为 10% 样本数。
m2 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
config = list(gwdr_config(0.2))
)
m2
Geographically Weighted Density Regression Model
================================================
Formula: PURCHASE ~ FLOORSZ + UNEMPLOY + PROF
Data: LondonHP
Dimension-specified Weighting Configuration
-------------------------------------------
bw unit kernel
X 0.200 % gaussian
Y 0.200 % gaussian
Summary of Coefficient Estimates
--------------------------------
Coefficient Min. 1st Qu. Median 3rd Qu. Max.
Intercept -376593.420 -186375.440 -102639.928 -40136.756 137723.988
FLOORSZ 901.315 1087.524 1522.518 1814.121 2840.217
UNEMPLOY -1317745.171 41504.759 435909.050 901915.439 2879552.062
PROF -127720.501 164473.936 249050.551 342561.859 540884.522
Diagnostic Information
----------------------
RSS: 272604534599
ENP: 61.61364
EDF: 254.3864
R2: 0.8477754
R2adj: 0.8107603
AIC: 7445.853
AICc: 7512.849
同样的,也可以使用 rep 函数,但是要确保传入正确的 times 变量的值。
m2 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
config = rep(gwdr_config(0.2), times = 2)
)
分别设置
如果分别设置加权配置项,则需要传入包含与自变量(如果有截距也包括截距)相同数量的 GWDRConfig 对象的列表。
m3 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
config = list(gwdr_config(bw = 0.5, kernel = "bisquare"),
gwdr_config(bw = 0.5, kernel = "bisquare"))
)
m3
Geographically Weighted Density Regression Model
================================================
Formula: PURCHASE ~ FLOORSZ + UNEMPLOY + PROF
Data: LondonHP
Dimension-specified Weighting Configuration
-------------------------------------------
bw unit kernel
X 0.500 % bisquare
Y 0.500 % bisquare
Summary of Coefficient Estimates
--------------------------------
Coefficient Min. 1st Qu. Median 3rd Qu. Max.
Intercept -338426.177 -197024.579 -108199.954 -21037.803 208405.791
FLOORSZ 874.665 1072.247 1441.932 1985.522 2578.291
UNEMPLOY -1684702.891 69860.819 502047.559 1278249.674 2274323.253
PROF -239863.434 149223.990 261570.242 368237.155 667653.133
Diagnostic Information
----------------------
RSS: 300737152296
ENP: 50.34853
EDF: 265.6515
R2: 0.8320659
R2adj: 0.8001173
AIC: 7469.247
AICc: 7523.108
这样就可以通过使用 c() rep() 等函数的组合灵活设置每个变量的配置项。
带宽优选
GWDR 模型的带宽优选必须要有一个初始值,所以即使让函数自动优选带宽,也要通过 config 参数指定带宽的类型和初始值。可以使用下面的方式启用带宽优选。
m4 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
optim_bw = "AIC"
)
带宽设置支持通过字符串 "AIC" 或 "CV" 设置带宽优选方法。
如果 config 参数指定的带宽初始值不合适(过大或过小),程序会自动设置为默认的初始值:可变带宽情况下是 61.8% 样本数,固定带宽情况下是该维度下最大坐标差的 61.8%。
模型优选
使用 model_sel() 函数可以对 gwdrm 对象进行模型优选。 如果使用的是 R 4.1 及以上版本,原生支持 |> 管道运算符,可以使用如下调用方式
m5 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
optim_bw = "AIC"
) |> model_sel(criterion = "AIC", threshold = 10, optim_bw = "AIC")
其中参数 threshold 表示指标值变化的阈值,由于目前内核库仅支持 AIC 指标选模型,因此参数 criterion 仅支持值 "AIC"。 如果使用的是低版本的 R,那么可使用下面的模式进行调用:
m5 <- gwdr(
PURCHASE ~ FLOORSZ + UNEMPLOY + PROF + BATH2 + BEDS2 + GARAGE1 +
TYPEDETCH + TPSEMIDTCH + TYPETRRD + TYPEBNGLW + BLDPWW1 +
BLDPOSTW + BLD60S + BLD70S + BLD80S + CENTHEAT,
LondonHP, optim_bw = "AIC"
)
m5 <- model_sel(m5, criterion = "AIC", threshold = 10, optim_bw = "AIC")
m5
函数 model_sel() 中也可以设置 config 参数。如果不设置,则继承 gwdrm 对象中的带宽大小、带宽类型、核函数的设置。如果这里设置了,则覆盖原有设置。进一步地,如果制定了 optim_bw 参数,则在模型优选完成后再进行带宽优选。
经过变量优选的模型返回值,包含一个与该函数同名的 $model_sel 变量,里面保存了模型优选过程中所有模型组合及其指标值。 包中提供了三个函数用于可视化该变量。
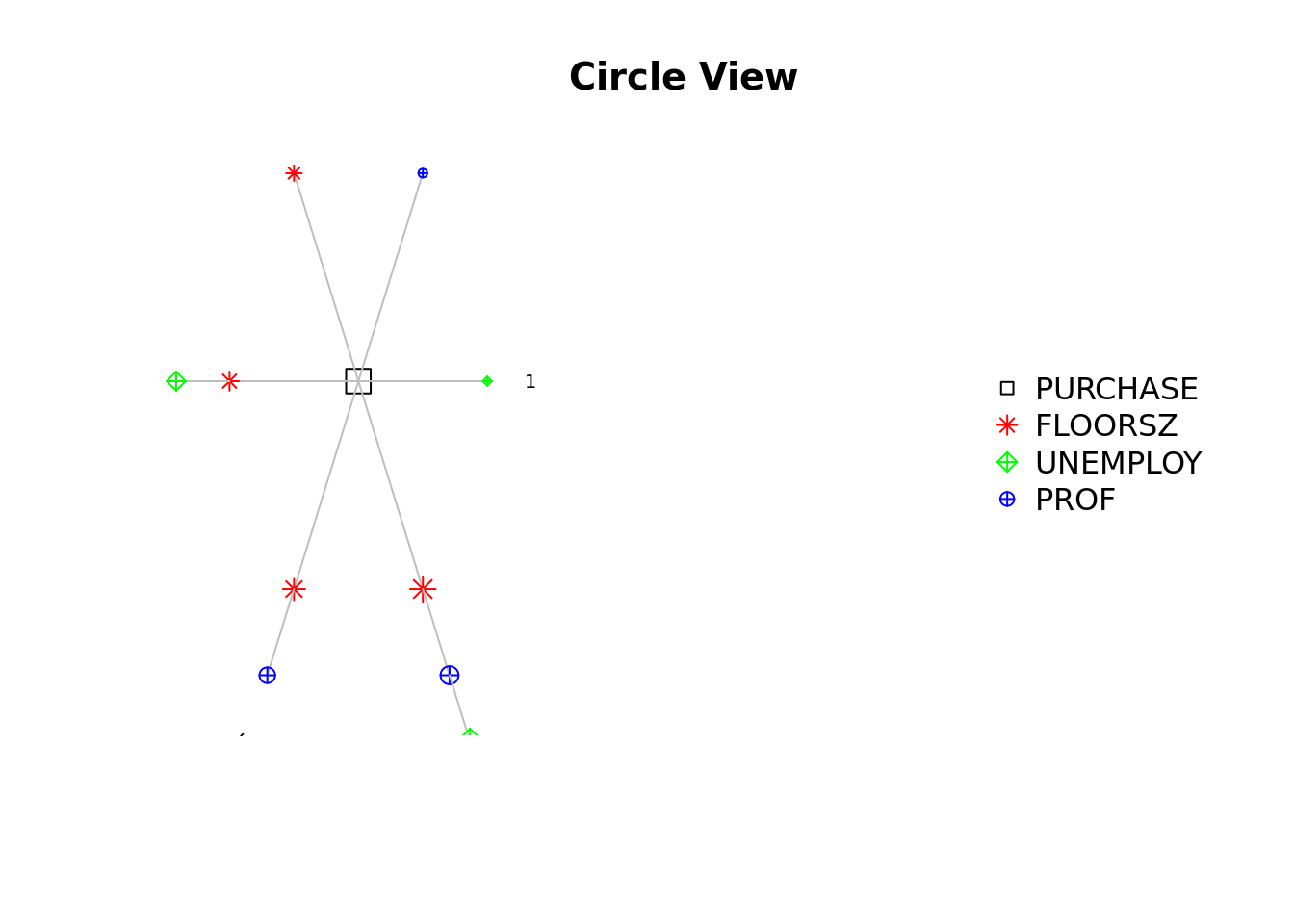
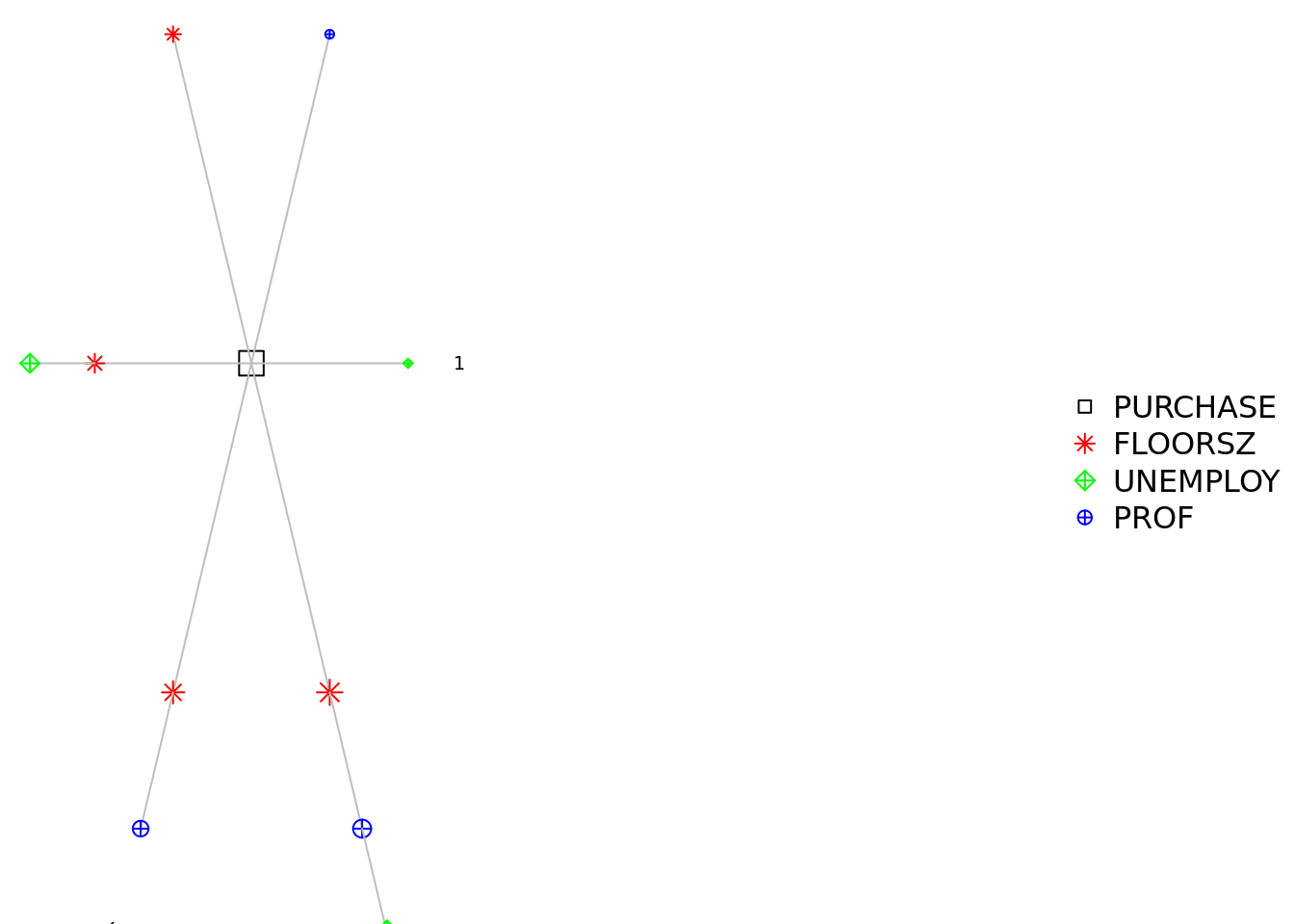
model_sel_view_circle(m5$model_sel, main = "Circle View")
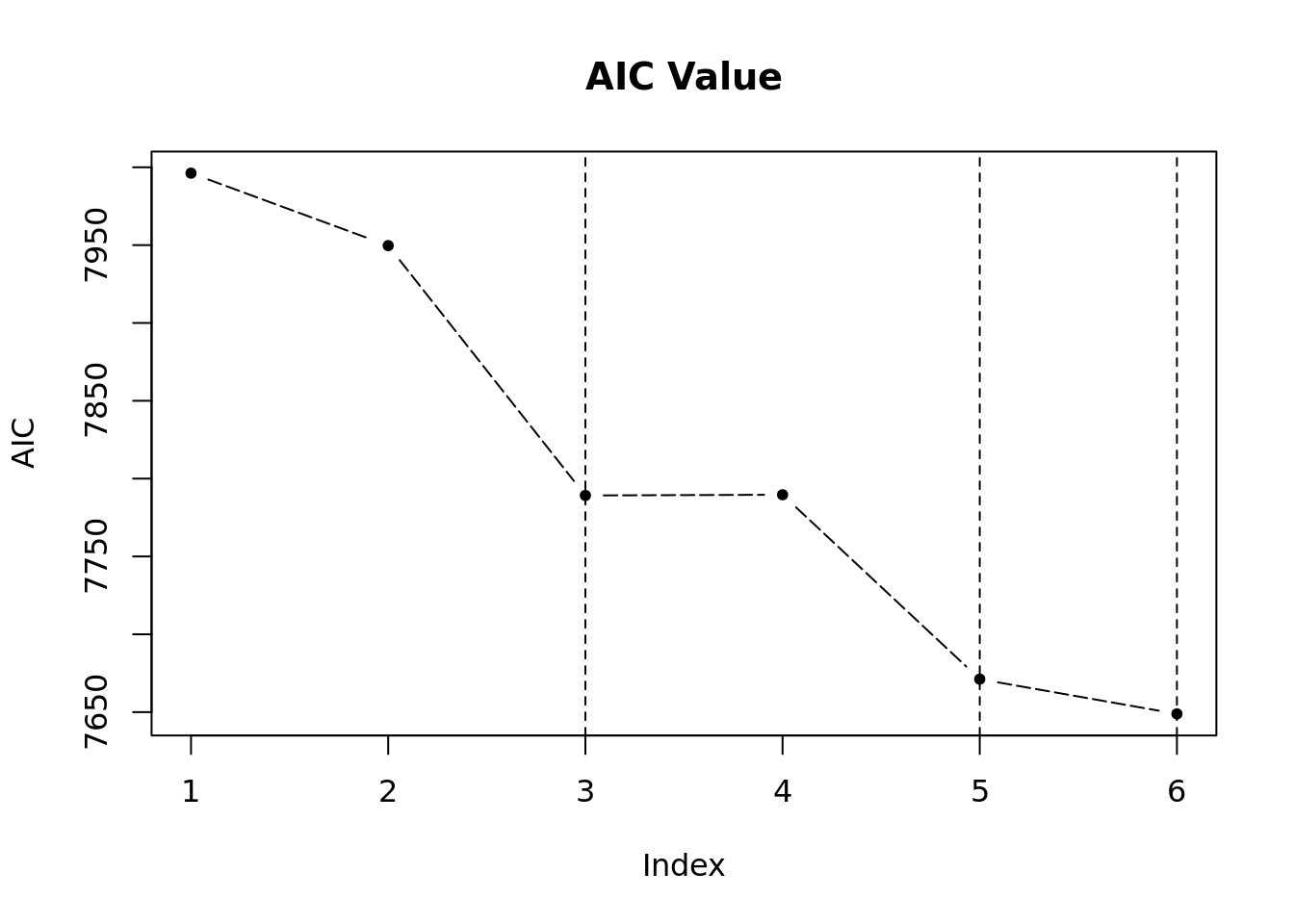
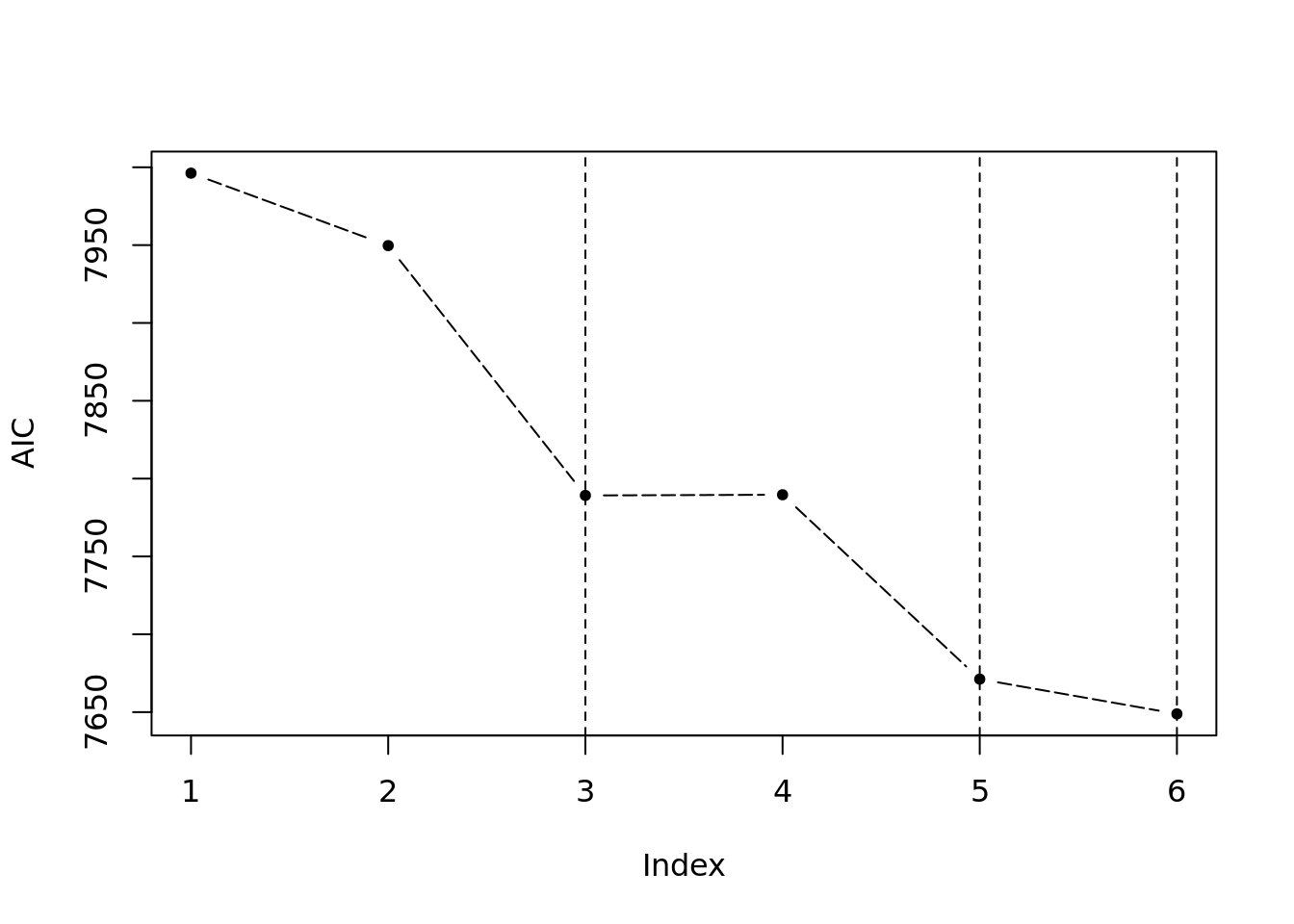
model_sel_view_value(m5$model_sel, main = "AIC Value")
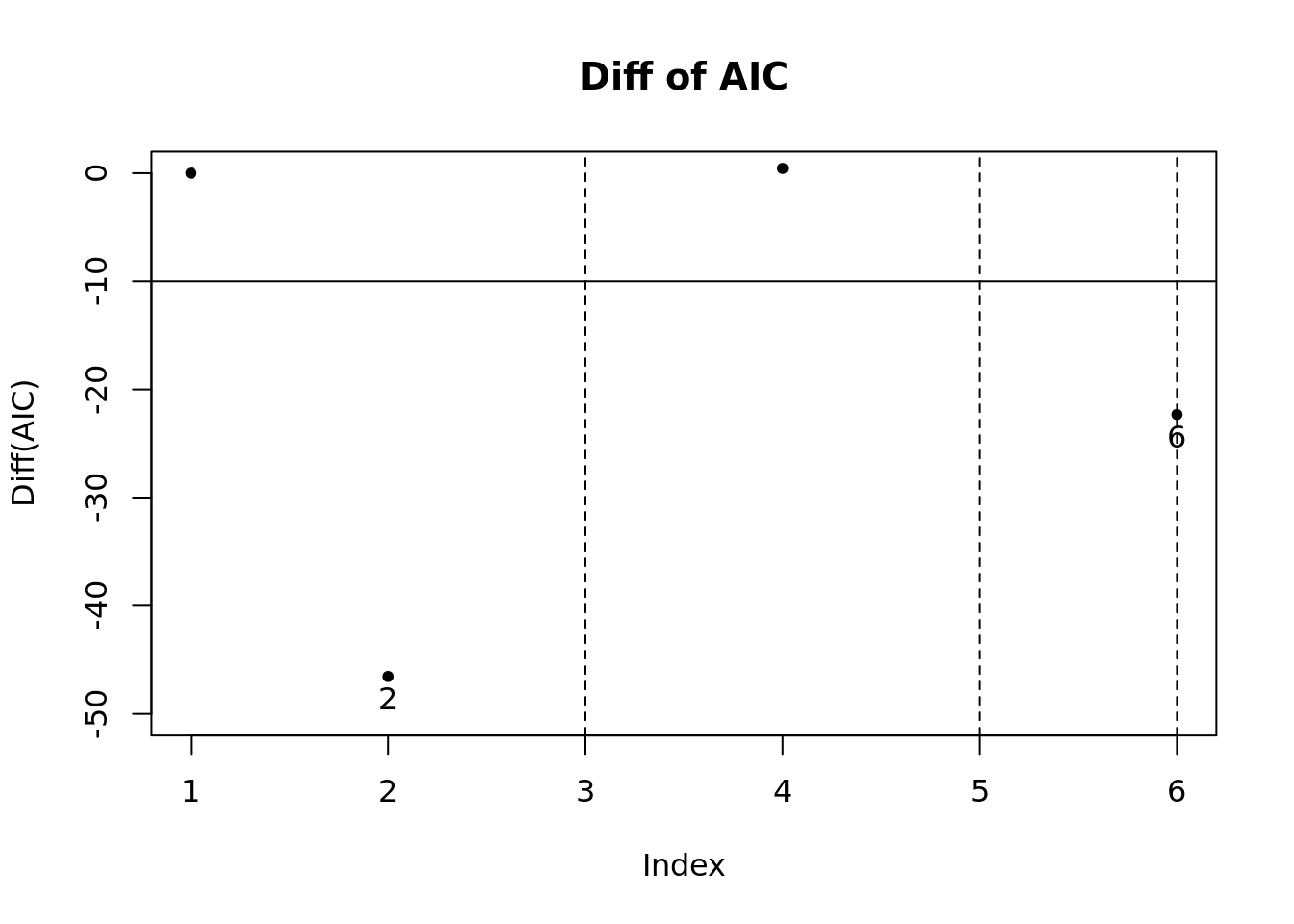
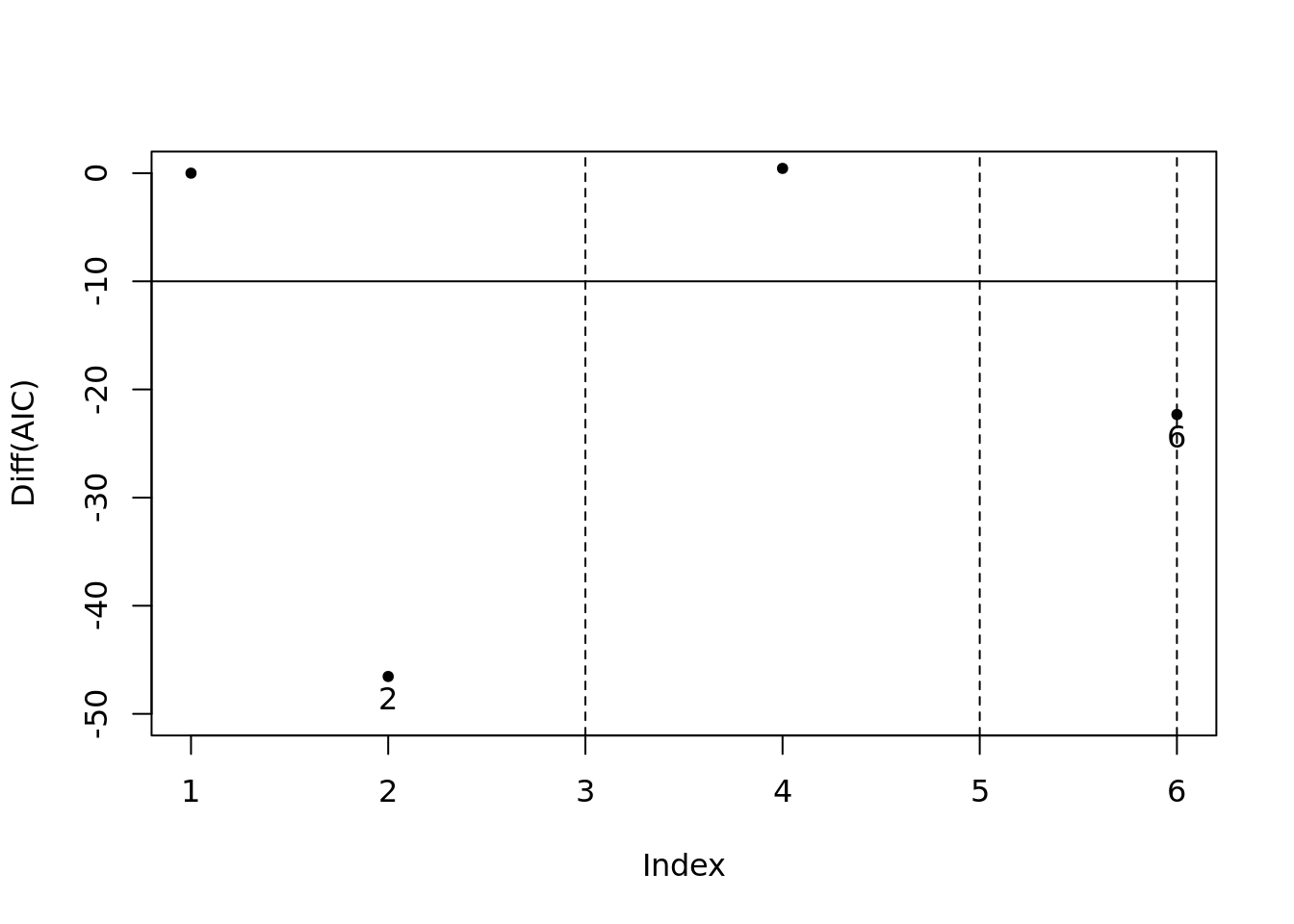
model_sel_view_diff(m5$model_sel, main = "Diff of AIC")
这三幅图分别为:
- 模型变量组合环形图。
- 模型指标值折线图。
- 模型指标值差分图。这个图是为了便于观察哪个模型符合阈值的要求。 图中所展示的数据是每个模型的指标值与上一个模型的指标值相比的变化情况(除了第一个默认为0)。 通过该图可以清晰地看到那些模型与上一个模型相比具有显著改进效果。
除了直接调用这三个函数之外,还可以统一使用 plot() 函数,该函数会做一些布局上的调整,以方便出图。
plot(m5$model_sel) # 等价于 model_sel_view_circle
plot(m5$model_sel, view = "value") # 等价于 model_sel_view_value
plot(m5$model_sel, view = "diff") # 等价于 model_sel_view_diff
如果想要进一步调整图片,可以直接添加其他被 plot() 函数支持的参数,例如图名 main 等。