本文主要介绍函数 gwr_basic() 的用法。
模型解算
我们以示例数据 LondonHP 为例,展示函数 gwr_basic() 的用法。 假设我们以 PURCHASE 为因变量,FLOORSZ, PROF 和 UNEMPLOY 为自变量,可以使用下面的方式构建 GWR 模型。
data(LondonHP)
m1 <- gwr_basic(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
bw = 64,
adaptive = TRUE
)
m1
Geographically Weighted Regression Model
========================================
Formula: PURCHASE ~ FLOORSZ + UNEMPLOY + PROF
Data: LondonHP
Kernel: gaussian
Bandwidth: 64 (Nearest Neighbours)
Summary of Coefficient Estimates
--------------------------------
Coefficient Min. 1st Qu. Median 3rd Qu. Max.
Intercept -198642.679 -182675.271 -165665.781 -134650.946 -93550.292
FLOORSZ 1189.823 1309.140 1399.934 1668.918 1840.670
UNEMPLOY 311994.460 531503.077 663356.786 735359.196 932328.652
PROF 243840.288 319870.143 355123.025 378312.489 429390.257
Diagnostic Information
----------------------
RSS: 4.56323e+11
ENP: 14.12809
EDF: 301.8719
R2: 0.7451855
R2adj: 0.7332201
AIC: 7571.953
AICc: 7585.417
与 GWmodel 相比,用法主要发生了以下变动:
- 函数名从
gwr.basic 改为 gwr_basic ,这是为了避免新旧版本包函数名称出现冲突,便于开发和测试。
- 该函数不再支持设置
regression.points 参数。该参数实现的功能将移到 predict() 函数中进行实现。
- 返回结果的展示发生了变化,去掉了线性回归的部分。 主要是为了使用户可以更灵活地设置
lm() 的参数,并避免显示信息过长导致不利于在 Jupyter 等环境中使用。
该函数返回一个 gwrm 的对象,通过控制台输出信息,我们可以得到 调用的表达式、数据、带宽、核函数、系数估计值的统计、诊断信息。 同样,也支持使用 coef() fitted() residuals() 等函数获取信息。
Intercept FLOORSZ UNEMPLOY PROF
0 -124453.6 1287.804 528674.5 295482.3
1 -122812.0 1282.712 520067.3 293203.2
2 -122487.0 1281.506 530303.5 291236.4
3 -121768.6 1278.788 527744.3 290153.6
4 -122064.9 1278.969 520144.8 291861.3
5 -101753.7 1234.532 396245.5 263582.0
[1] 135011.1 132297.2 117858.7 157436.0 173050.9 157071.0
[1] 21988.936 -18797.233 -36108.677 -7436.005 16949.120 2879.028
此外,与旧版 GWmodel 包类似,gwrm 对象中提供了一个 $SDF 变量保存了系数估计值等一系列局部结果。
Simple feature collection with 6 features and 14 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 531900 ymin: 159400 xmax: 535700 ymax: 161700
CRS: NA
Intercept FLOORSZ UNEMPLOY PROF yhat residual Intercept.SE
0 -124453.6 1287.804 528674.5 295482.3 135011.1 21988.936 5839925
1 -122812.0 1282.712 520067.3 293203.2 132297.2 -18797.233 5873318
2 -122487.0 1281.506 530303.5 291236.4 117858.7 -36108.677 5962947
3 -121768.6 1278.788 527744.3 290153.6 157436.0 -7436.005 5990687
4 -122064.9 1278.969 520144.8 291861.3 173050.9 16949.120 5928749
5 -101753.7 1234.532 396245.5 263582.0 157071.0 2879.028 6126740
FLOORSZ.SE UNEMPLOY.SE PROF.SE Intercept.TV FLOORSZ.TV UNEMPLOY.TV
0 351842.1 14680113 7170057 -0.02131082 0.003660175 0.03601297
1 353135.2 14735103 7214234 -0.02091015 0.003632355 0.03529444
2 356231.7 14939953 7324666 -0.02054135 0.003597394 0.03549566
3 357162.0 14994222 7360524 -0.02032632 0.003580416 0.03519651
4 354868.2 14840291 7285505 -0.02058864 0.003604066 0.03504950
5 363613.1 15108910 7586125 -0.01660813 0.003395180 0.02622595
PROF.TV geometry
0 0.04121060 POINT (533200 159400)
1 0.04064233 POINT (533300 159700)
2 0.03976104 POINT (532000 159800)
3 0.03942024 POINT (531900 160100)
4 0.04006054 POINT (532800 160300)
5 0.03474527 POINT (535700 161700)
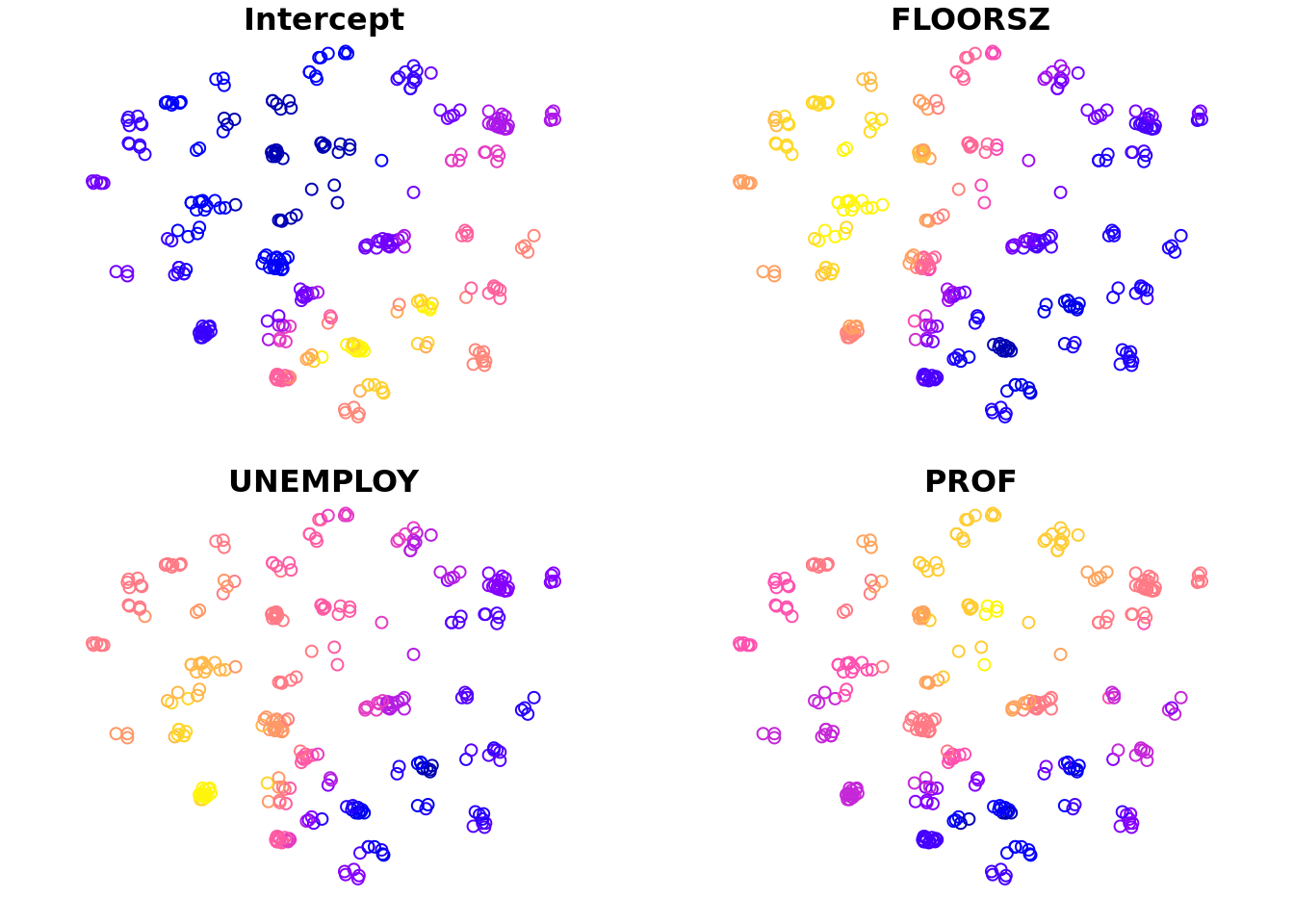
使用该变量,可以进行专题制图。除此之外,改包还提供了一个 plot() 函数,通过输入 gwrm 对象,可以快速查看回归系数。
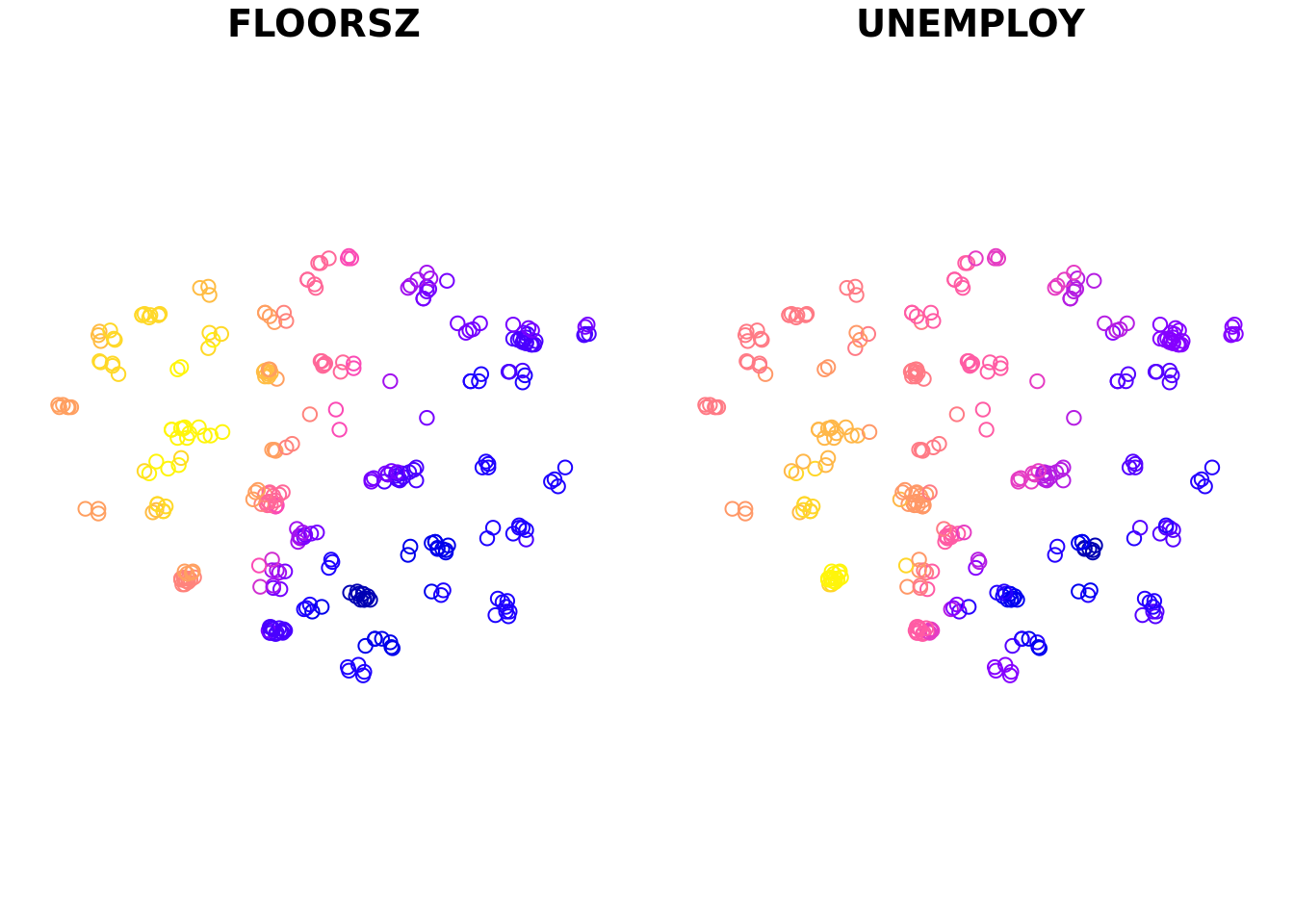
plot(m1, columns = c("FLOORSZ", "UNEMPLOY"))
如果指定了 columns 参数,则仅绘制第二个参数列出的系数,否则绘制所有回归系数。
带宽优选
如果希望系统自动优选一个带宽,而不是手动设置带宽大小,可以使用下面的方式调用函数。
m <- gwr_basic(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
bw = "AIC",
adaptive = TRUE
)
message("Bandwidth:", m$args$bw)
带宽设置支持通过字符串 "AIC" 或 "CV" 设置带宽优选方法。此外,如果参数 bw 不存在,或设置为非数值型变量, 程序也会根据 AIC 值自动优选带宽。用户不再需要调用单独的 bw.gwr() 函数手动优选带宽。
进行这样改动的原因是:
- 内核库中优选完带宽后直接进行了模型解算,而不是返回带宽值,节省一些手动拟合模型的时间。
- 避免参数在不同函数中重复设置,导致出现错误, 例如在
bw.gwr() 中将 adaptive 改成了 FALSE,但出于某些原因,忘记在 gwr.basic() 中同步修改,从而造成错误。
- 节省参数个数。因为带宽仅有指定、优选两种情况,因此可以根据
bw 的数据类型进行情况判断。 当 bw 是数值型变量时(包括 Inf),说明带宽已经指定,此时无需进行带宽优选; 当带宽需要优选时,又无法指定 bw 的具体值,因此可以用该参数表示带宽优选的指标类型。
如果要获取优选的带宽值,则通过函数返回对象中的 $args$bw 变量获取,或者从控制台输出返回对象信息读出。
模型优选
该部分的改动也比较大。 包中定义了一个 “Generic” 的函数 model_sel() (姑且称之为泛型函数), 当其作用与 gwrm 对象上时,表示对该拟合得到的模型进行变量优选。 其用法类似于 MASS 包中的 stepAIC() 函数。 在实际使用中,用户一般都是先拟合一个变量较多的模型,然后从中进行变量优选。 如果使用的是 R 4.1 及以上版本,原生支持 |> 管道运算符,可以使用如下调用方式
m2 <- gwr_basic(
PURCHASE ~ FLOORSZ + UNEMPLOY + PROF + BATH2 + BEDS2 + GARAGE1 +
TYPEDETCH + TPSEMIDTCH + TYPETRRD + TYPEBNGLW + BLDPWW1 +
BLDPOSTW + BLD60S + BLD70S + BLD80S + CENTHEAT,
LondonHP, "AIC", TRUE
) |> model_sel(criterion = "AIC", threshold = 10, bw = Inf, optim_bw = "AIC")
m2
Geographically Weighted Regression Model
========================================
Formula: PURCHASE ~ FLOORSZ + PROF + UNEMPLOY
Data: LondonHP
Kernel: gaussian
Bandwidth: 20 (Nearest Neighbours) (Optimized accroding to AIC)
Summary of Coefficient Estimates
--------------------------------
Coefficient Min. 1st Qu. Median 3rd Qu. Max.
Intercept -283403.492 -202450.678 -146322.221 -26250.365 75680.532
FLOORSZ 908.249 1095.711 1411.257 1864.155 2482.376
PROF -16595.354 143221.798 303155.382 379563.029 480351.828
UNEMPLOY -982984.259 -5935.799 575766.002 1029212.413 1780751.157
Diagnostic Information
----------------------
RSS: 348701748965
ENP: 40.26956
EDF: 275.7304
R2: 0.8052821
R2adj: 0.7767406
AIC: 7506.818
AICc: 7546.36
其中参数 threshold 表示指标值变化的阈值,由于目前内核库仅支持 AIC 指标选模型,因此参数 criterion 仅支持值 "AIC"。 如果使用的是低版本的 R,那么可使用下面的模式进行调用:
m2 <- gwr_basic(
PURCHASE ~ FLOORSZ + UNEMPLOY + PROF + BATH2 + BEDS2 + GARAGE1 +
TYPEDETCH + TPSEMIDTCH + TYPETRRD + TYPEBNGLW + BLDPWW1 +
BLDPOSTW + BLD60S + BLD70S + BLD80S + CENTHEAT,
LondonHP, "AIC", TRUE
)
m2 <- model_sel(m2, criterion = "AIC", threshold = 10, bw = Inf, optim_bw = "AIC")
m2
函数 model_sel() 中也有一个 bw 参数,同时也附加了一个 optim_bw 的参数。其用法是:
- 如果
bw 不设置或者是 NA,那么将采用传入的 gwrm 对象中记录的带宽值。
- 如果
bw 是数值型,使用该 bw 值作为模型优选中使用的带宽值。根据 optim_bw 的情况判断是否在解算前进行带宽优选。
- 如果
optim_bw 指定了 "no",那么默认以 AIC 作为指标进行带宽优选。
- 如果
optim_bw 指定了 "AIC" 或 "CV",那么以根据相应的指标进行带宽优选。
- 如果
bw 是非数值型值,则默认使用 Inf 值作为带宽进行变量优选,并在模型解算前,使用变量 optim_bw 指定的指标值进行变量优选。 但如果 optim_bw 指定了 "no",那么默认以 AIC 作为指标进行带宽优选。
虽然该逻辑看起来比较复杂,但是使用起来很简单。一般情况下,就使用如上设置的参数即可。
经过变量优选的模型返回值,包含一个与该函数同名的 $model_sel 变量,里面保存了模型优选过程中所有模型组合及其指标值。 包中提供了三个函数用于可视化该变量。
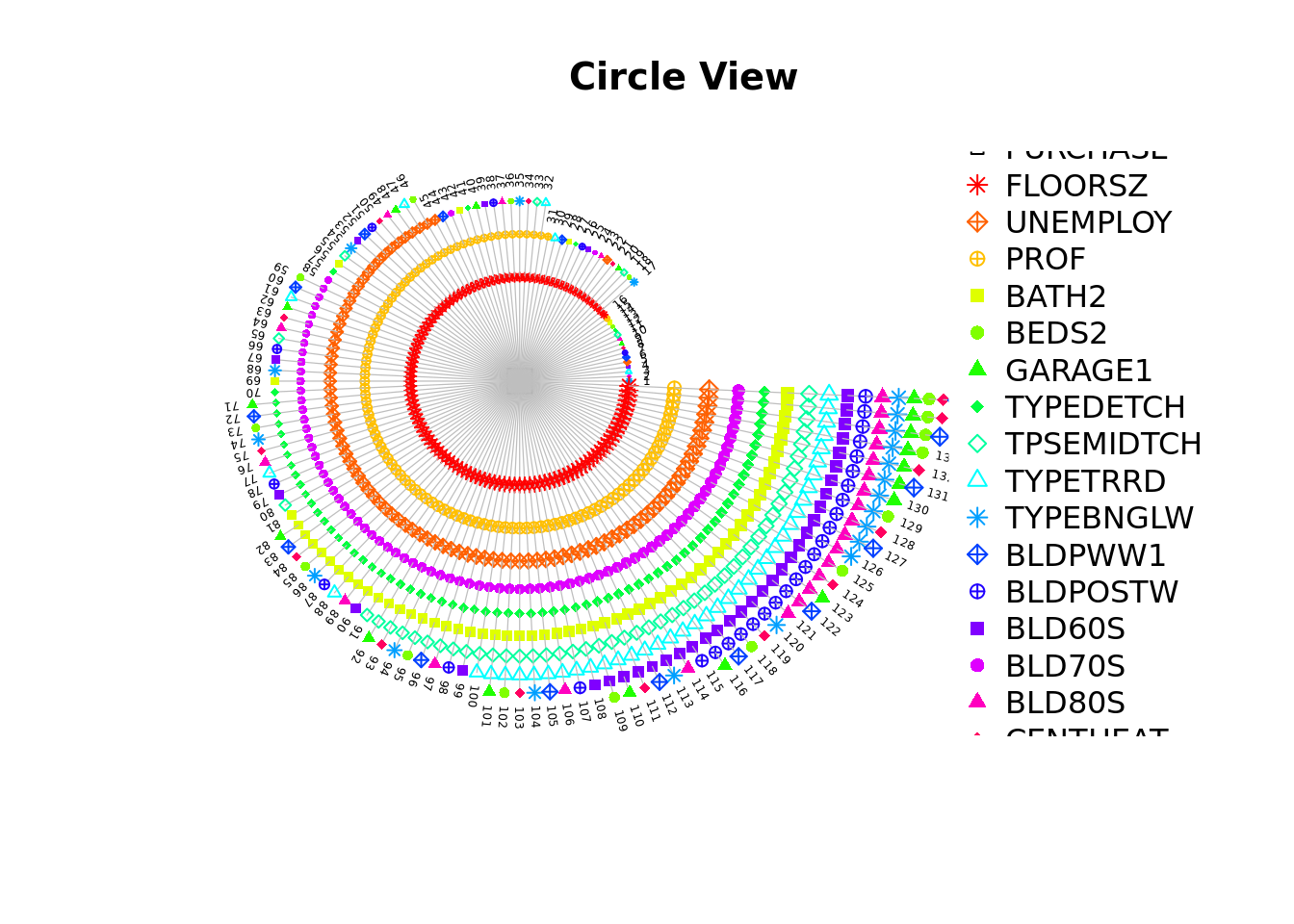
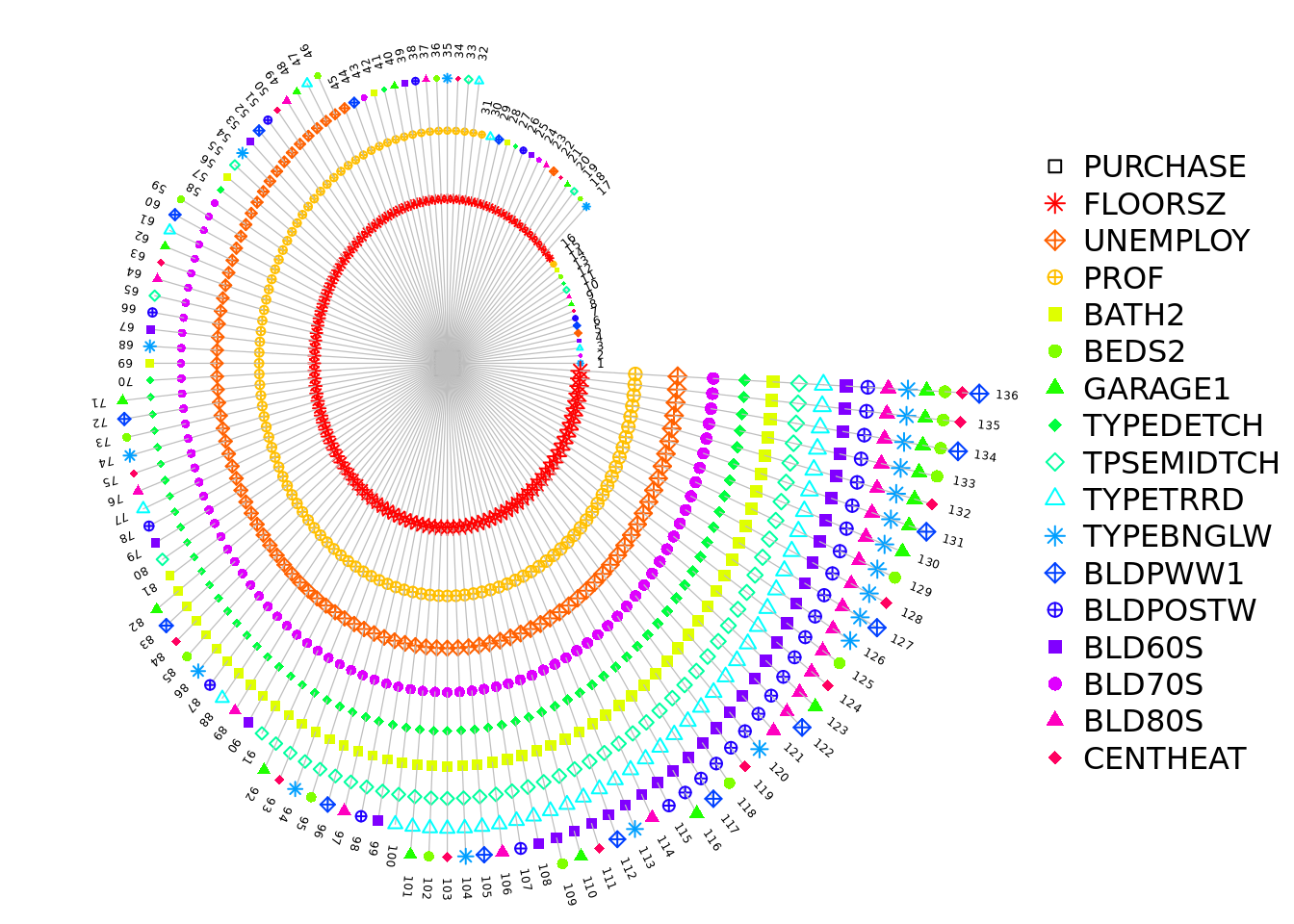
model_sel_view_circle(m2$model_sel, main = "Circle View")
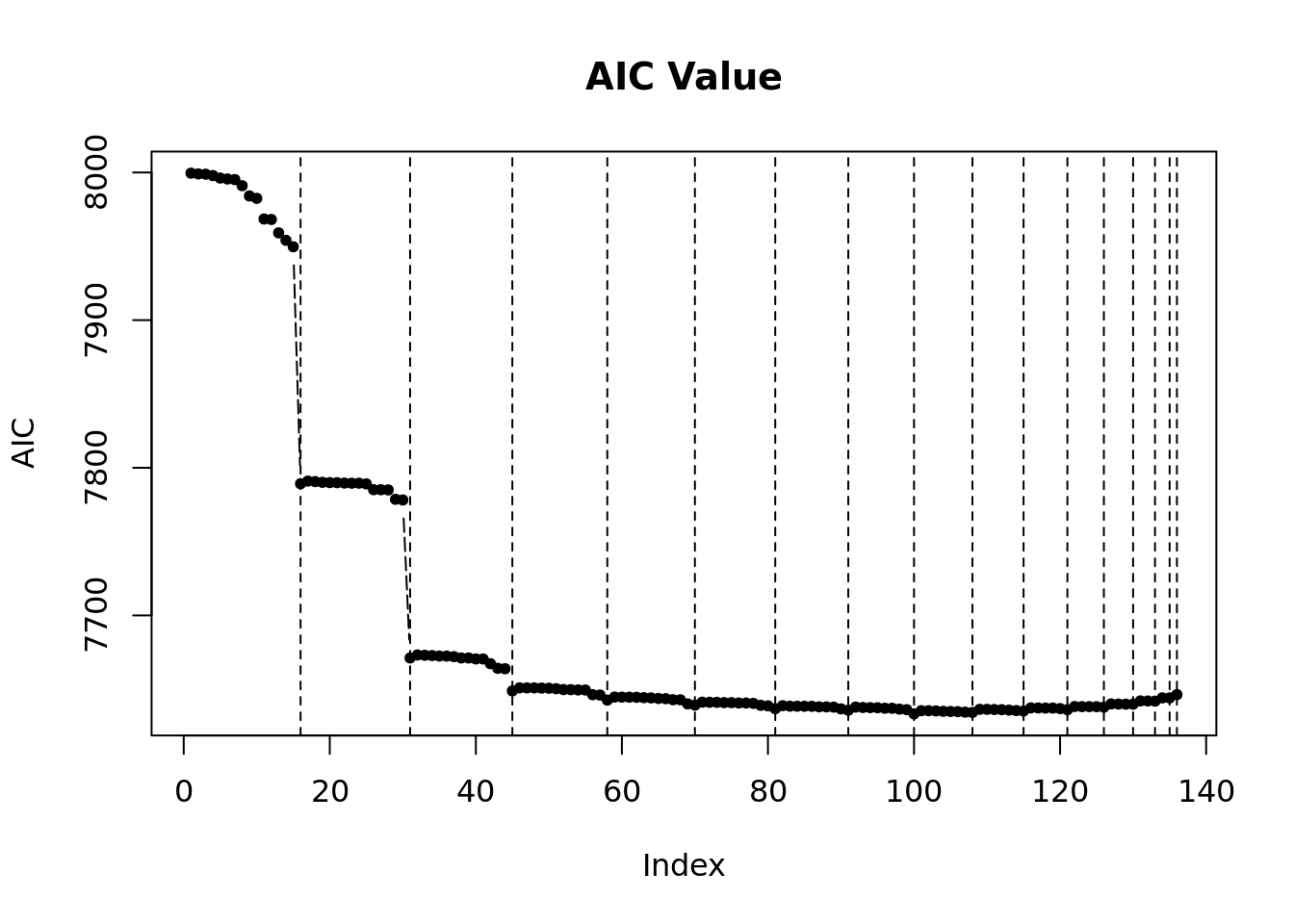
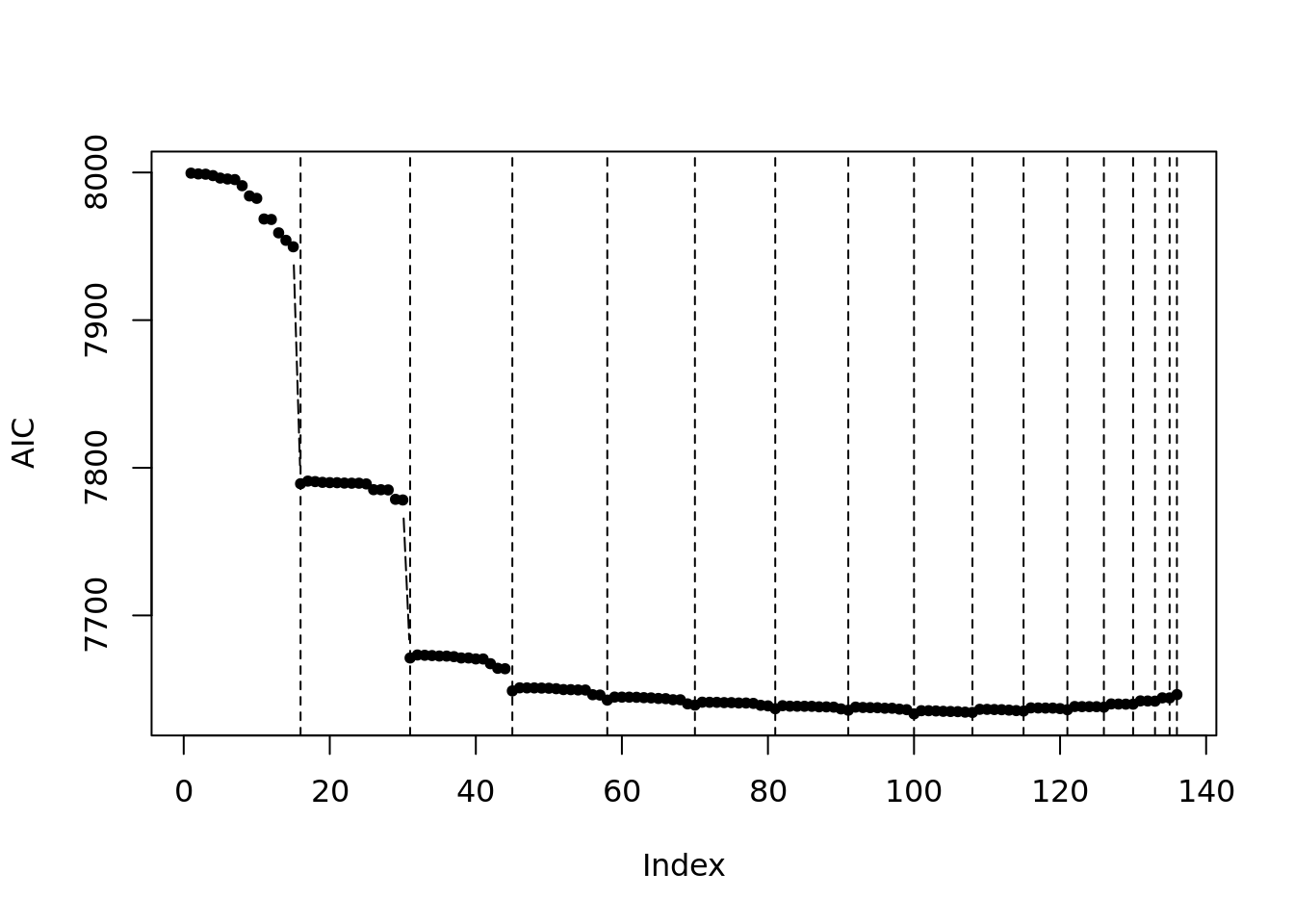
model_sel_view_value(m2$model_sel, main = "AIC Value")
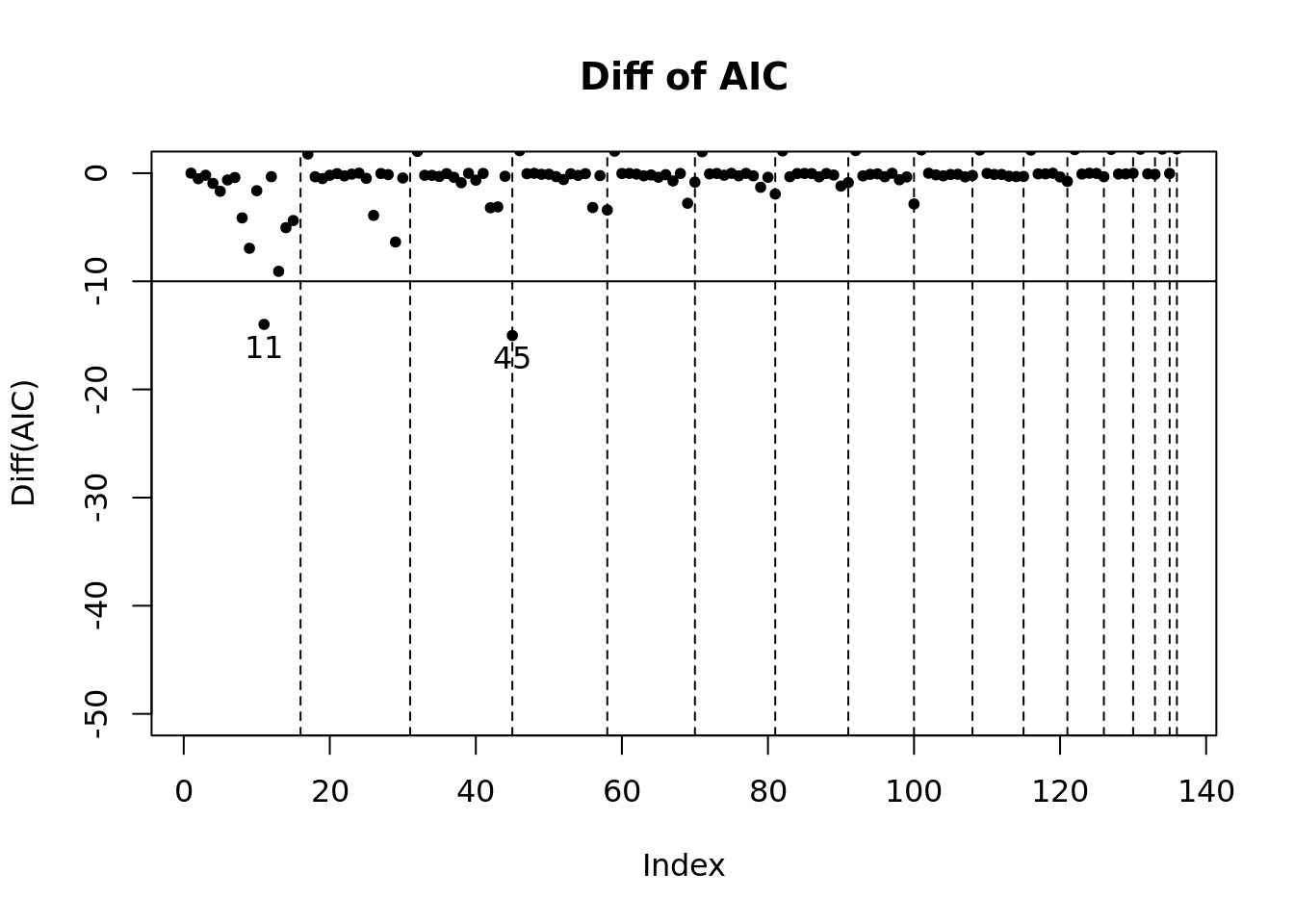
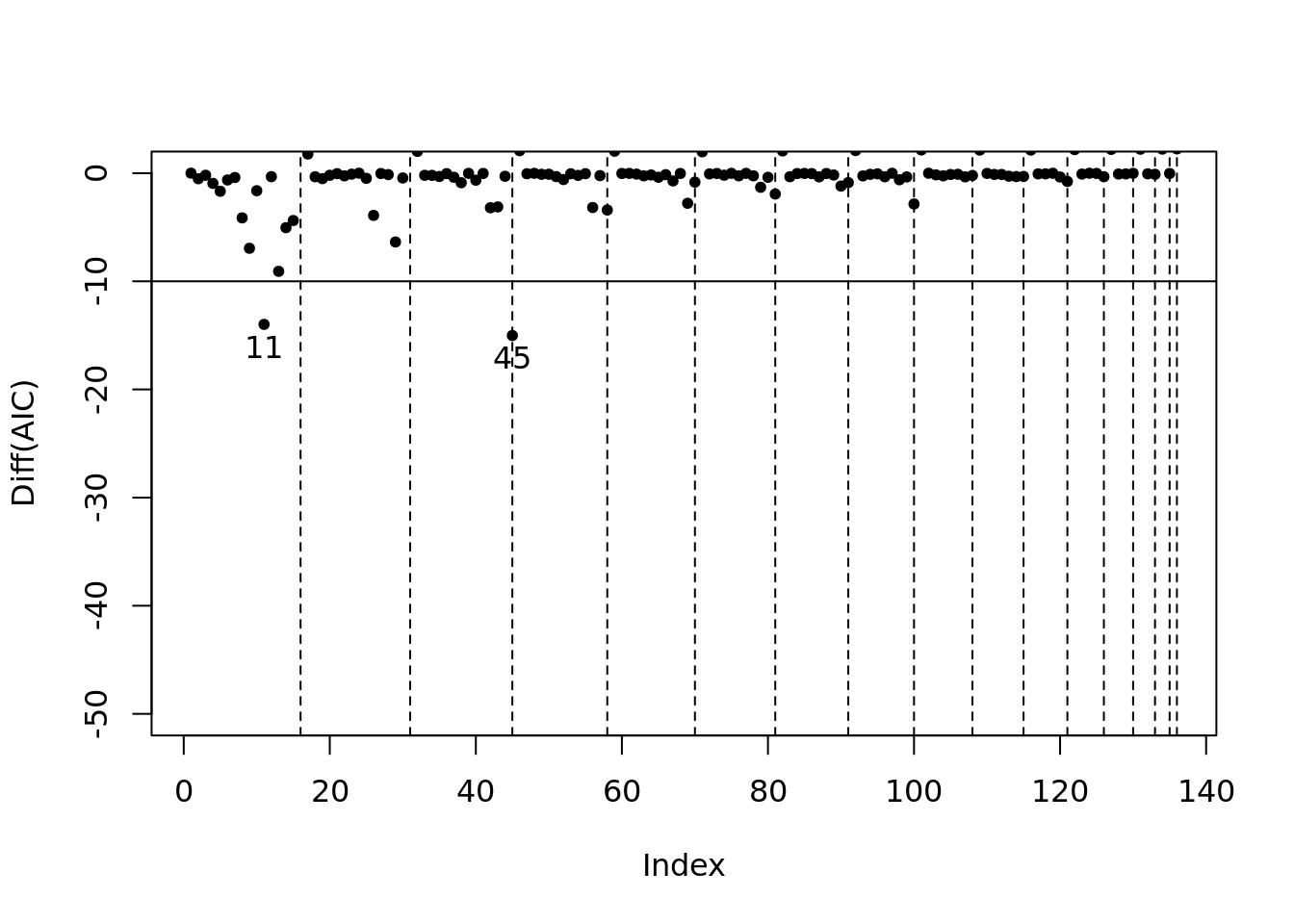
model_sel_view_diff(m2$model_sel, main = "Diff of AIC")
这三幅图分别为:
- 模型变量组合环形图。
- 模型指标值折线图。
- 模型指标值差分图。这个图是为了便于观察哪个模型符合阈值的要求。 图中所展示的数据是每个模型的指标值与上一个模型的指标值相比的变化情况(除了第一个默认为0)。 通过该图可以清晰地看到那些模型与上一个模型相比具有显著改进效果。
除了直接调用这三个函数之外,还可以统一使用 plot() 函数,该函数会做一些布局上的调整,以方便出图。
plot(m2$model_sel) # 等价于 model_sel_view_circle
plot(m2$model_sel, view = "value") # 等价于 model_sel_view_value
plot(m2$model_sel, view = "diff") # 等价于 model_sel_view_diff
如果想要进一步调整图片,可以直接添加其他被 plot() 函数支持的参数,例如图名 main 等。
预测
根据已有模型,GWR 可以在任意点的位置进行回归系数和预测。所需要用到的函数是 predict() 函数。 我们这里直接使用原数据集进行预测。
Simple feature collection with 316 features and 6 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 507400 ymin: 159400 xmax: 552300 ymax: 194900
CRS: NA
First 10 features:
Intercept FLOORSZ PROF UNEMPLOY yhat residual
0 -23859.461 1107.8783 143091.28 -68568.68 127499.2 29500.837
1 -19273.643 1099.6911 137317.02 -105774.02 125164.0 -11664.024
2 -22341.033 1101.6762 139576.72 -78733.42 112173.3 -30423.269
3 -16587.207 1091.7319 131959.65 -127715.69 145741.0 4259.021
4 -4548.212 1071.6907 118805.43 -236130.77 158572.5 31427.480
5 36721.681 1025.9964 69162.51 -574801.77 158491.4 1458.602
6 41385.027 1015.8069 64587.38 -621772.02 139520.0 10475.019
7 41586.375 980.2804 72971.83 -702105.05 206972.8 32977.160
8 57682.066 985.6583 47493.74 -778290.44 158200.9 -5200.854
9 71221.072 928.7546 43974.22 -982984.26 310010.7 -60060.651
geometry
0 POINT (533200 159400)
1 POINT (533300 159700)
2 POINT (532000 159800)
3 POINT (531900 160100)
4 POINT (532800 160300)
5 POINT (535700 161700)
6 POINT (535600 161800)
7 POINT (533400 161900)
8 POINT (535500 162200)
9 POINT (534200 162500)
根据传入的第二个参数的类型不同,该函数会给出不同的结果:
- 如果第二个参数是一个
sf 或 sfc 类型对象,该函数返回一个 sf 或 sfc 类型的对象, 其中包含了原始数据的几何信息。
- 如果第二个参数只是一个两列的
matrix 或 data.frame,那么该函数返回一个 data.frame 对象, 不包含几何信息,但与输入数据行数一致。
此外,如果第二个参数是一个 sf 或 sfc 类型对象,返回值的内容会根据该参数中包含的数据变化:
- 如果参数中不包含完整的自变量字段,那么仅返回系数估计值;
- 如果参数中包含完整的自变量字段,但不包含因变量字段,除了返回系数估计值外还返回因变量估计值;
- 如果参数中包含完整的自变量字段,也包含因变量字段,除了返回系数估计值外还返回因变量估计值和残差。
这样可以根据不同的需求获取不同的结果。