Geographically weighted density regression (GWDR), is a model which calcaulates a wight for each dimension of coordinates, and calibrate regression model with the product of these weights. In this page, we mainly introduce the usage of gwdr().
library(sf)
#> Linking to GEOS 3.7.1, GDAL 2.4.0, PROJ 5.2.0; sf_use_s2() is TRUE
library(GWmodel3)
#>
#> Attaching package: 'GWmodel3'
#> The following object is masked from 'package:stats':
#>
#> stepBasics
Let us set the data LondonHP as an example, and show how to use gwdr(). Assume that the PURCHASE is the dependent variable, while FLOORSZ, PROF and UNEMPLOY are independent variable, we can calibrate a GWDR model with the following code.
data(LondonHP)
m1 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP
)
m1
#> Geographically Weighted Density Regression Model
#> ================================================
#> Formula: PURCHASE ~ FLOORSZ + UNEMPLOY + PROF
#> Data: LondonHP
#> Dimension-specified Weighting Configuration
#> -------------------------------------------
#> bw unit kernel
#> X 0.618 % gaussian
#> Y 0.618 % gaussian
#>
#>
#> Summary of Coefficient Estimates
#> --------------------------------
#> Coefficient Min. 1st Qu. Median 3rd Qu. Max.
#> Intercept -193327.404 -175567.666 -168977.411 -162922.380 -140786.788
#> FLOORSZ 1305.212 1393.038 1467.604 1576.467 1696.385
#> UNEMPLOY 523550.252 580577.144 642590.758 718386.733 824739.610
#> PROF 330854.107 351258.803 368915.791 388013.724 413800.564
#>
#>
#> Diagnostic Information
#> ----------------------
#> RSS: 494470388228
#> ENP: 10.34202
#> EDF: 305.658
#> R2: 0.7238836
#> R2adj: 0.7145105
#> AIC: 7594.609
#> AICc: 7604.972Here no additional arguments are set, so the function will apply the follwing configurations:
- Banwdith size for each dimension is 61.8% samples.
- Adaptive bandwidth for each dimension.
- Gaussian kernel function for each dimension.
- No bandwidth optimization.
On most situations, these configurations can ensure the algorithm works. To further specify arguments, please turn to Weighting configurations.
This function returns a object of class name gwdrm. Through the outputs in console, we can get infromation of fomula, data, kernel, bandwidth, coefficient estimates, and diagnostics. Besides, it is supported to get more infromation via coef() fitted() residuals().
head(coef(m1))
#> Intercept FLOORSZ UNEMPLOY PROF
#> 0 -156686.3 1360.666 665222.6 349001.4
#> 1 -156301.6 1358.544 662711.3 348652.4
#> 2 -159630.9 1375.525 687318.5 351295.0
#> 3 -159754.8 1376.436 688396.9 351320.4
#> 4 -157435.6 1362.784 671656.0 349629.5
#> 5 -146554.7 1311.270 601273.5 339194.4
head(fitted(m1))
#> [1] 138878.6 136126.3 121082.4 163737.0 179706.1 160977.9
head(residuals(m1))
#> [1] 18121.366 -22626.252 -39332.379 -13737.003 10293.939 -1027.876Like other functions, gwdrm objects provide a $SDF variable which contains coefficient estimates and other sample-wise results.
head(m1$SDF)
#> Simple feature collection with 6 features and 6 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: 531900 ymin: 159400 xmax: 535700 ymax: 161700
#> CRS: NA
#> Intercept FLOORSZ UNEMPLOY PROF yhat residual
#> 0 -156686.3 1360.666 665222.6 349001.4 138878.6 18121.366
#> 1 -156301.6 1358.544 662711.3 348652.4 136126.3 -22626.252
#> 2 -159630.9 1375.525 687318.5 351295.0 121082.4 -39332.379
#> 3 -159754.8 1376.436 688396.9 351320.4 163737.0 -13737.003
#> 4 -157435.6 1362.784 671656.0 349629.5 179706.1 10293.939
#> 5 -146554.7 1311.270 601273.5 339194.4 160977.9 -1027.876
#> geometry
#> 0 POINT (533200 159400)
#> 1 POINT (533300 159700)
#> 2 POINT (532000 159800)
#> 3 POINT (531900 160100)
#> 4 POINT (532800 160300)
#> 5 POINT (535700 161700)We can create maps with this variable. There is a plot() function provided to preview coefficient estimates easily.
plot(m1)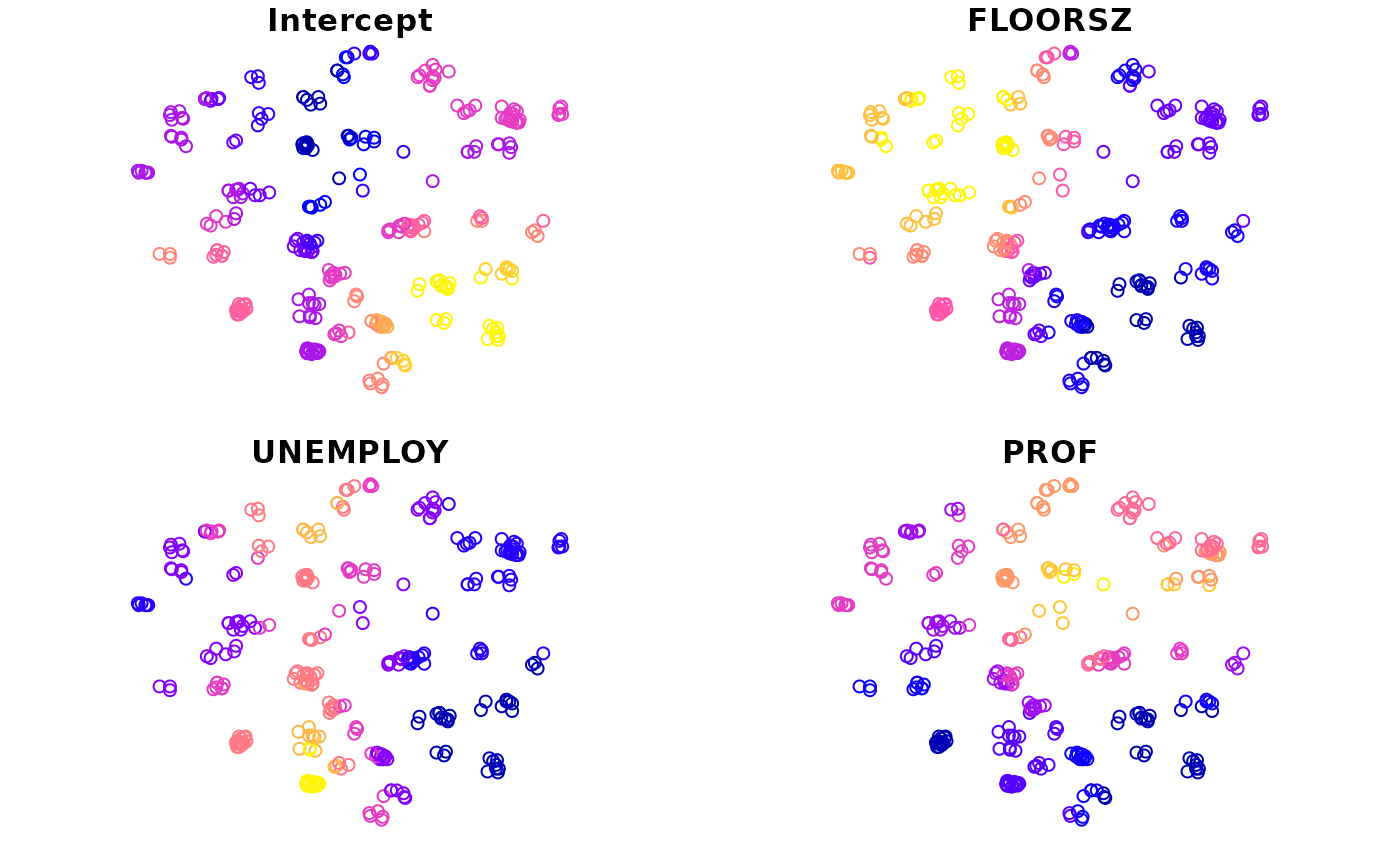

If the second argument is omitted, all coefficient estimates will be mapped by default. Otherwise, only specified variables will be mapped.
Weighting configurations
S4 class for dimension-specified weighting configrations
This package provides a S4 class named GWDRConfig, which is used to set dimension-specified weighting configurations. This class contains the following slots:
| Slot | Type | Descirption |
|---|---|---|
bw |
Numeric | Banwdith size. |
adaptive |
Logical | Whether the bandwidth is adaptive. |
kernel |
Character | Name of the kernel function. |
We can use the function gwdr_config() to create an object.
gwdr_config(0.618, TRUE, "bisquare")
#> An object of class "GWDRConfig"
#> Slot "bw":
#> [1] 0.618
#>
#> Slot "adaptive":
#> [1] TRUE
#>
#> Slot "kernel":
#> [1] "bisquare"Replicating via rep() is enabled, but only the times parameter is supported.
rep(gwdr_config(36, TRUE, "bisquare"), 2)
#> [[1]]
#> An object of class "GWDRConfig"
#> Slot "bw":
#> [1] 36
#>
#> Slot "adaptive":
#> [1] TRUE
#>
#> Slot "kernel":
#> [1] "bisquare"
#>
#>
#> [[2]]
#> An object of class "GWDRConfig"
#> Slot "bw":
#> [1] 36
#>
#> Slot "adaptive":
#> [1] TRUE
#>
#> Slot "kernel":
#> [1] "bisquare"Use GWDRConfig to configure arguments
The function gwdr() can not only set a uniform configuration, but also set each a configuration for dimensions.
Uniform configuration
To set a uniform configuration for all dimensions, just pass a list of only one GWDRConfig object. For example, the following code will set the bandwidth size to 10% samples for all dimensions.
m2 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
config = list(gwdr_config(0.2))
)
m2
#> Geographically Weighted Density Regression Model
#> ================================================
#> Formula: PURCHASE ~ FLOORSZ + UNEMPLOY + PROF
#> Data: LondonHP
#> Dimension-specified Weighting Configuration
#> -------------------------------------------
#> bw unit kernel
#> X 0.200 % gaussian
#> Y 0.200 % gaussian
#>
#>
#> Summary of Coefficient Estimates
#> --------------------------------
#> Coefficient Min. 1st Qu. Median 3rd Qu. Max.
#> Intercept -376593.420 -186375.440 -102639.928 -40136.756 137723.988
#> FLOORSZ 901.315 1087.524 1522.518 1814.121 2840.217
#> UNEMPLOY -1317745.171 41504.759 435909.050 901915.439 2879552.062
#> PROF -127720.501 164473.936 249050.551 342561.859 540884.522
#>
#>
#> Diagnostic Information
#> ----------------------
#> RSS: 272604534599
#> ENP: 61.61364
#> EDF: 254.3864
#> R2: 0.8477754
#> R2adj: 0.8107603
#> AIC: 7445.853
#> AICc: 7512.849Likewise, we can use the rep() function, but remember to use a right times argument, which should be equal to the number of independent variables (including the intercept if it exists).
m2 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
config = rep(gwdr_config(0.2), times = 2)
)Separate configuration
To set configurations separately for each dimension, we need to input a list of GWDRConfig objects with the same number of elements to that of dimensions.
m3 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
config = list(gwdr_config(bw = 0.5, kernel = "bisquare"),
gwdr_config(bw = 0.5, kernel = "bisquare"))
)
m3
#> Geographically Weighted Density Regression Model
#> ================================================
#> Formula: PURCHASE ~ FLOORSZ + UNEMPLOY + PROF
#> Data: LondonHP
#> Dimension-specified Weighting Configuration
#> -------------------------------------------
#> bw unit kernel
#> X 0.500 % bisquare
#> Y 0.500 % bisquare
#>
#>
#> Summary of Coefficient Estimates
#> --------------------------------
#> Coefficient Min. 1st Qu. Median 3rd Qu. Max.
#> Intercept -338426.177 -197024.579 -108199.954 -21037.803 208405.791
#> FLOORSZ 874.665 1072.247 1441.932 1985.522 2578.291
#> UNEMPLOY -1684702.891 69860.819 502047.559 1278249.674 2274323.253
#> PROF -239863.434 149223.990 261570.242 368237.155 667653.133
#>
#>
#> Diagnostic Information
#> ----------------------
#> RSS: 300737152296
#> ENP: 50.34853
#> EDF: 265.6515
#> R2: 0.8320659
#> R2adj: 0.8001173
#> AIC: 7469.247
#> AICc: 7523.108Then the functions c() rep() can be used to flexiably create such a list.
Bandwidth Optimization
The bandwidth optimization algorithm for GWDR requires a set of initial values for each parameter. Thus, even bandwidth optimization is enabled, it is necessary to set the initial values via the config argument. We can enable bandwidth optimization with the following codes.
m4 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
optim_bw = "AIC"
)The method for optimizing bandwidth is specified through strings "AIC" or "CV". If the initial values are not appropriate, the function will use the default initial values instead: 61.8% samples for adaptive bandwidth, while 61.8% of maximum distance between samples for fixed bandwidth.
Model Selection
Apply the step() function to gwdrm objects to select the best model. Since version 4.1 of R, the pipe operator |> is avaliable. We can use the following code to enable model selection.
m5 <- gwdr(
formula = PURCHASE ~ FLOORSZ + UNEMPLOY + PROF,
data = LondonHP,
optim_bw = "AIC"
) |> step(criterion = "AIC", threshold = 3, optim_bw = "AIC")Where argument threshold is the threshold showing minimum changes of the criterion. Currently, only AIC criterion is supported, so the criterion here can only be "AIC".
For R of lower version, please use the following form:
m5 <- gwdr(
PURCHASE ~ FLOORSZ + UNEMPLOY + PROF + BATH2 + BEDS2,
LondonHP, optim_bw = "AIC"
)
m5 <- step(m5, criterion = "AIC", threshold = 10, optim_bw = "AIC")
m5
#> Geographically Weighted Density Regression Model
#> ================================================
#> Formula: PURCHASE ~ FLOORSZ + PROF + UNEMPLOY
#> Data: LondonHP
#> Dimension-specified Weighting Configuration
#> -------------------------------------------
#> bw unit kernel
#> X 0.155 % gaussian
#> Y 0.196 % gaussian
#>
#>
#> Summary of Coefficient Estimates
#> --------------------------------
#> Coefficient Min. 1st Qu. Median 3rd Qu. Max.
#> Intercept -610710.092 -185729.218 -87371.104 -10904.357 252299.605
#> FLOORSZ 846.945 1058.576 1475.677 1914.966 3486.379
#> PROF -324882.636 89042.360 197398.378 313394.073 913105.451
#> UNEMPLOY -1996220.111 -223025.550 255246.558 1313205.723 6641280.360
#>
#>
#> Diagnostic Information
#> ----------------------
#> RSS: 209784782000
#> ENP: 85.57122
#> EDF: 230.4288
#> R2: 0.8828544
#> R2adj: 0.8391621
#> AIC: 7383.702
#> AICc: 7492.59We can set config in step() to overwrite the original configurations. If it is not set, configurations in the gwdrm object will be applied. Further, if optim_bw is sepcified, bandwidth will be optimized afther the model selection.
The returned object after model selection contains a $step variable, in which there are all model combinations and corresponding criterions. There are three functions to visualize it.
step_view_circle(m5$step, main = "Circle View")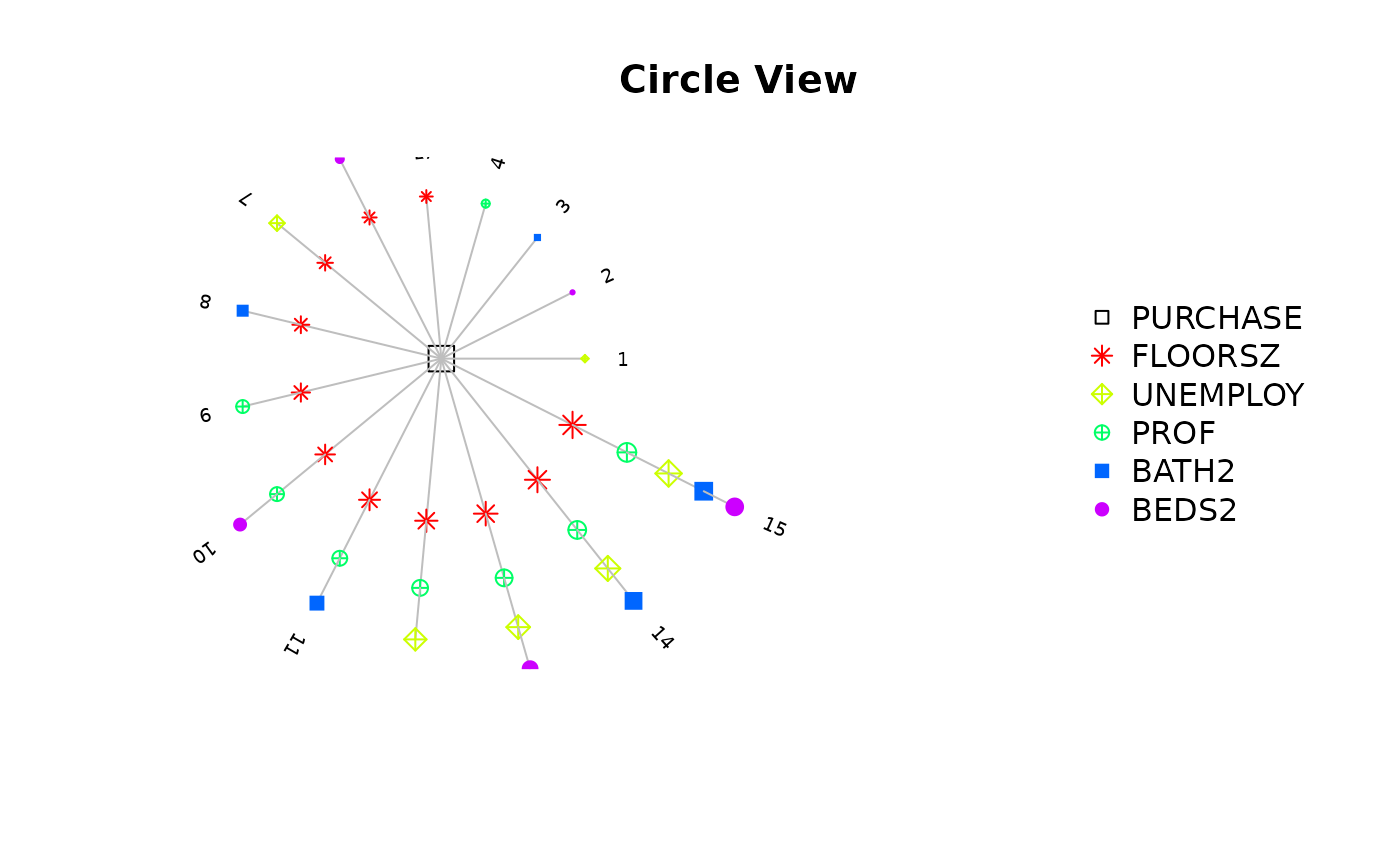
step_view_value(m5$step, main = "AIC Value")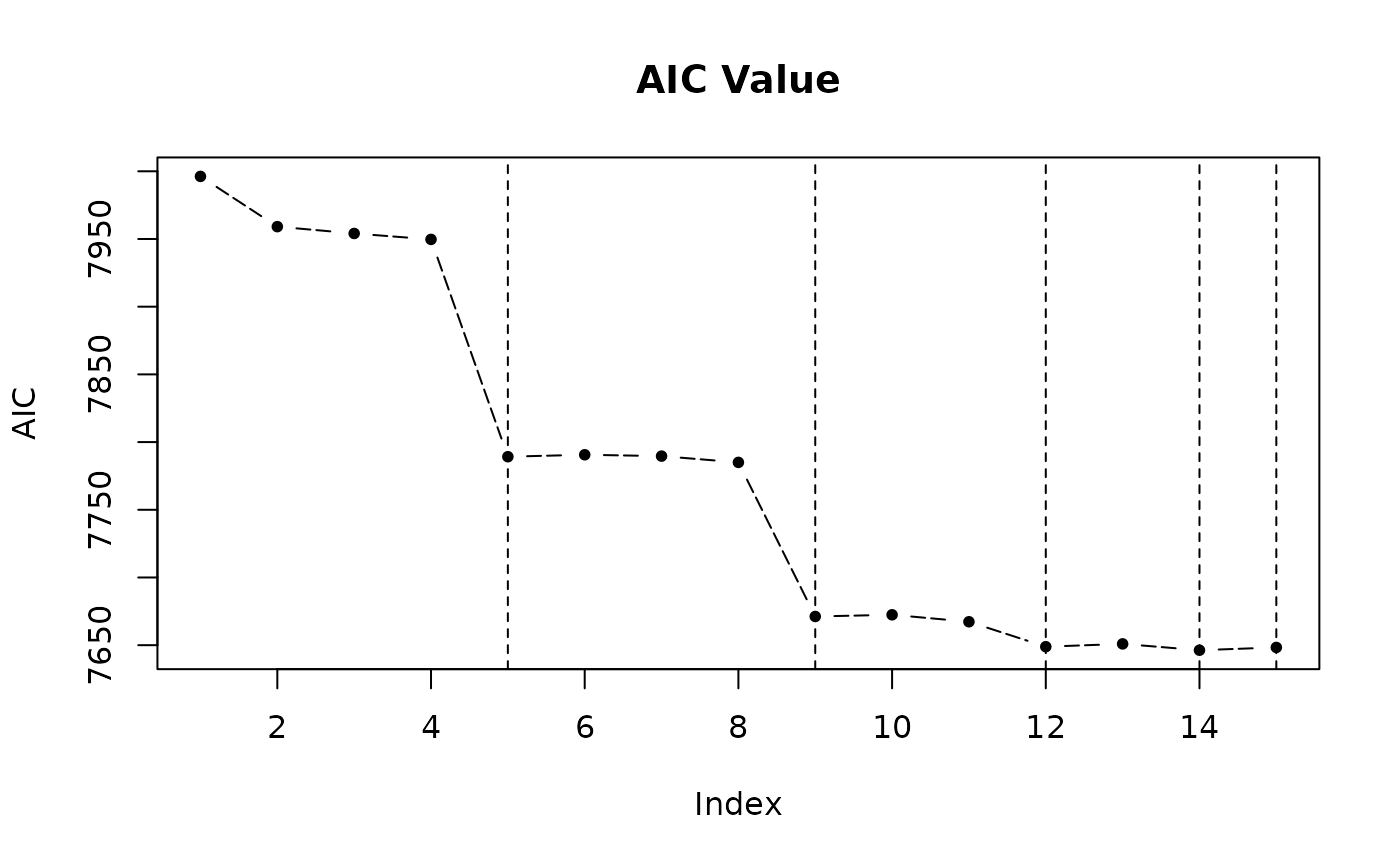
step_view_diff(m5$step, main = "Diff of AIC")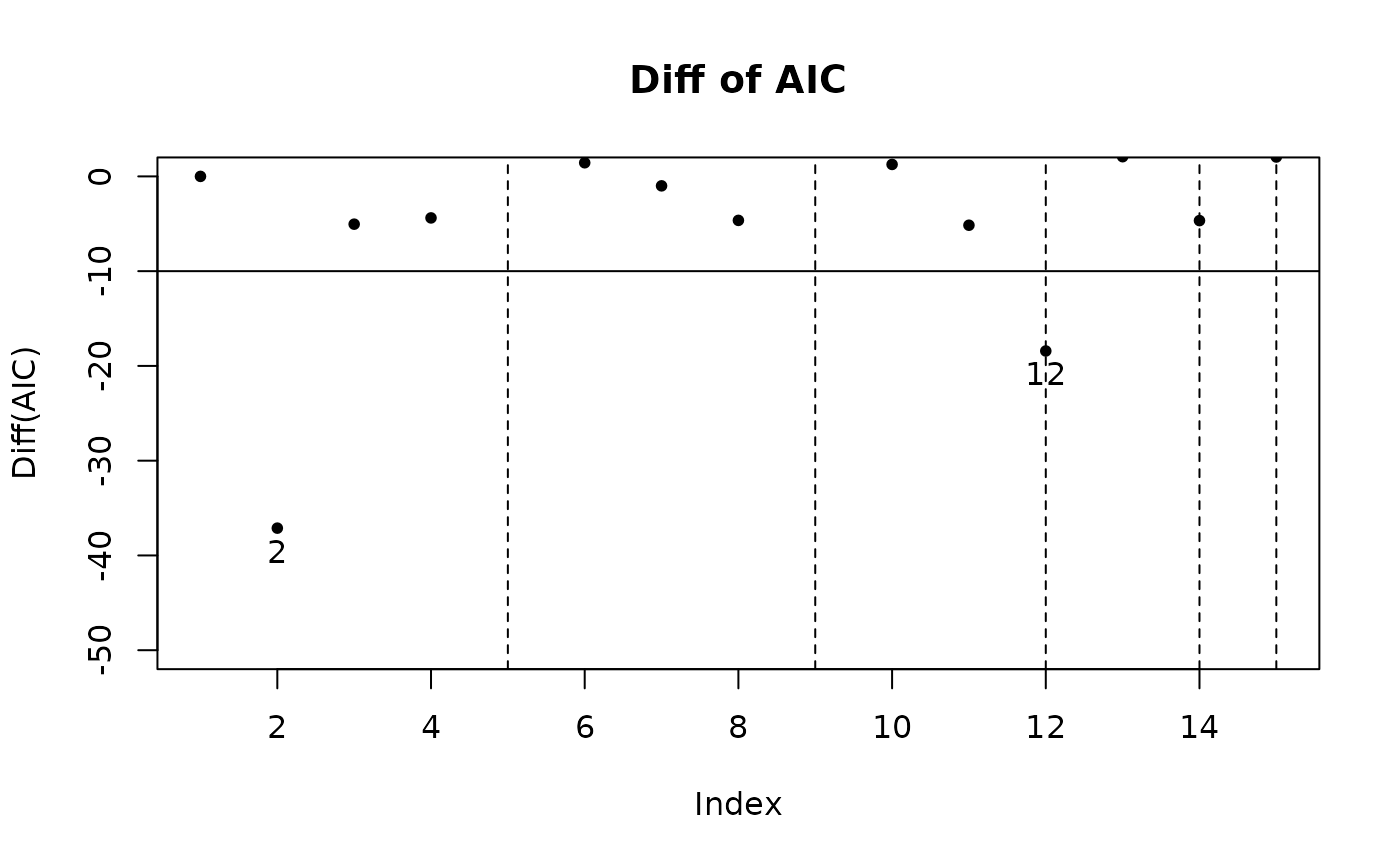
They are:
- Variable combinations.
- Criterions for each combination.
- Difference of criterions. The improvement in the criterion for each combination compared with the previous one is clearly shown. This figure makes it easier to judge which model meets the requirement.
We can also use the universal plot() function which will make some modification to layouts.
plot(m5$step) # 等价于 step_view_circle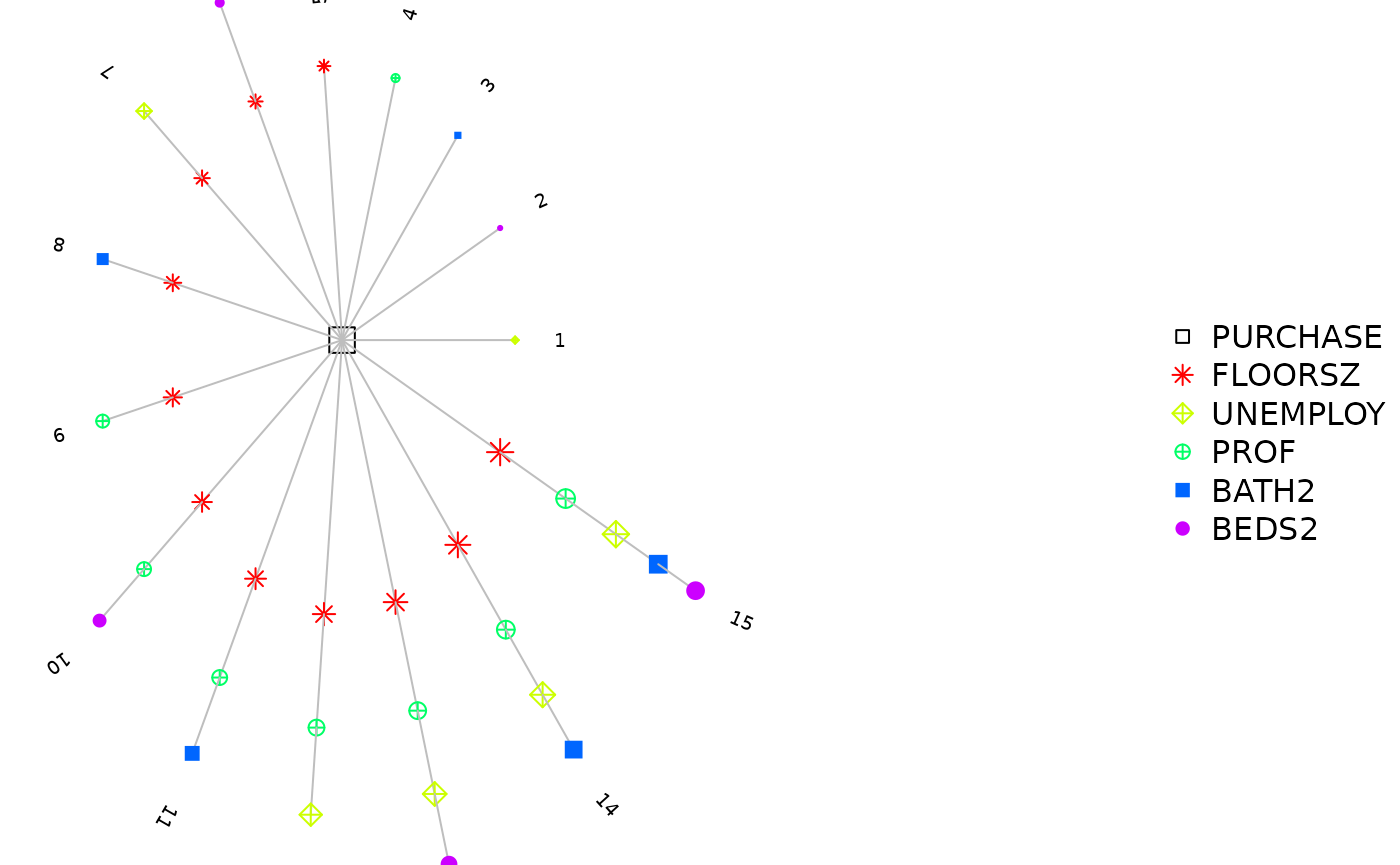
plot(m5$step, view = "value") # 等价于 step_view_value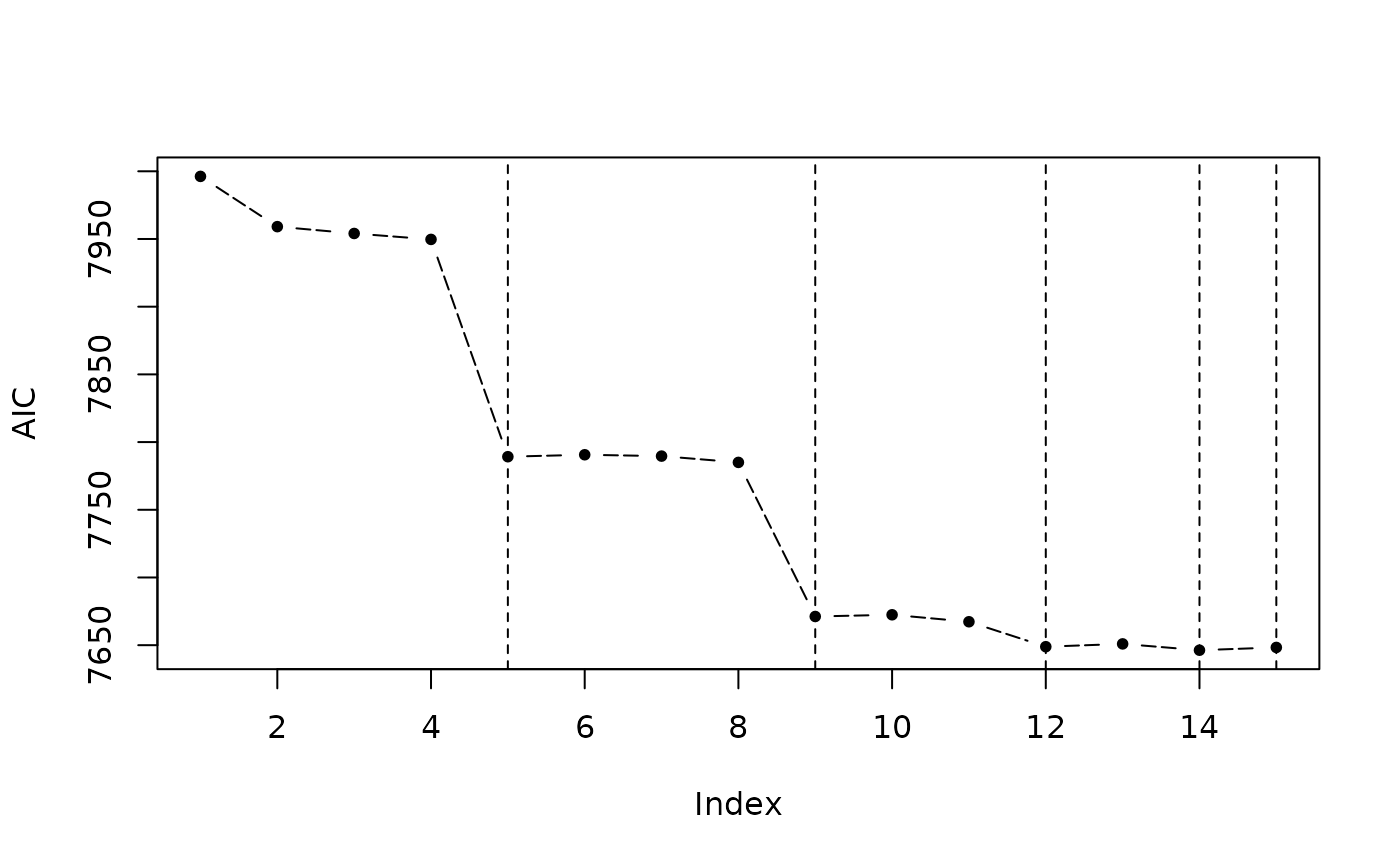
plot(m5$step, view = "diff") # 等价于 step_view_diff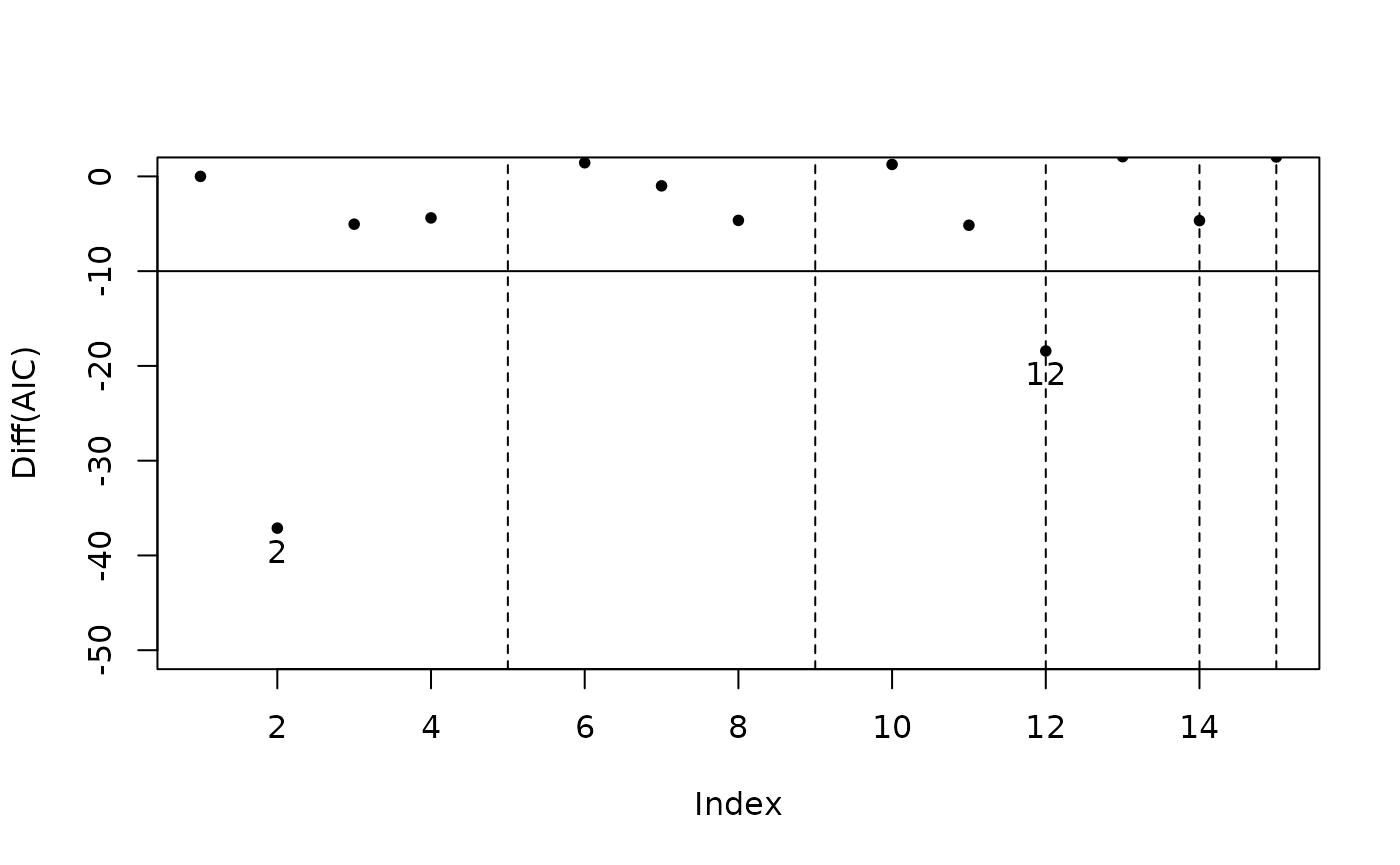
If further modification is required, use other arguments supported by plot().